Category:Electronic ground-state properties
At the end of an electronic minimization, VASP has obtained a converged set of orbitals (WAVECAR). Based on the orbitals also the corresponding density is computed via k-point integration (CHGCAR). The orbitals and the density reveal important insights into material properties and are often the first step towards analyzing and understanding a material.
An easy way to visualize the properties discussed below is using py4vasp.
Properties of orbitals
For practical purposes, one is most interested in the energy eigenvalues of the orbitals and their local projections. Consider first the eigenvalues: Counting all orbitals with eigenvalues in a certain energy interval yields the density of states (DOS) (DOSCAR). Often, looking at the DOS can provide valuable insight into the electronic properties of a material, e.g., an estimate of the electron itinerancy or specific heat. It is, therefore, often the first step to start towards understanding a novel material.
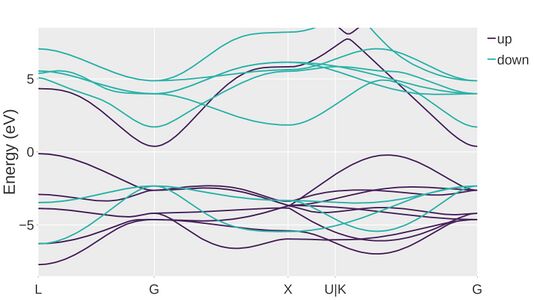
The band structure contains even more details about the electronic eigenvalues (EIGENVAL) by resolving them with respect to the Bloch vector k. Usually, one uses high-symmetry paths in the Brillouin zone for band structures. They make it easy to recognize fundamental and direct bandgaps of the material. Alternatively, VASP directly reports the bandgaps to the OUTCAR file with the verbosity controlled by the BANDGAP tag. The electronic eigenvalues determine the occupations of each orbital in conjunction with the settings for ISMEAR, SIGMA, and EFERMI.
Next, we consider the projections of the orbitals that you activate with the LORBIT tag. VASP projects each orbital onto functions with defined angular momentum within the PAW sphere of each ion. This site projection augments the data produced by DOS and band-structure calculations. In addition, the projections describe how much charge has a particular angular momentum and spin near an ion. This serves as a good approximation for the magnetic structure of the system.
Properties on the grid
The charge density is defined on a real-space grid in the unit cell and results from a sum over bands and k points of all occupied orbitals. The grid is often called FFT grid because the underlying calculation requires repeatedly switching between real and reciprocal space via FFTs on that grid. For magnetic calculations (ISPIN=2 or LNONCOLLINEAR=T), the orbitals and charge density have additional spin indices and include the magnetization. VASP stores the charge density in the CHGCAR file and can use it to restart a calculation (ICHARG≥10), which is particularly relevant for non-self-consistent calculations like band-structure calculations.
Most of the time, the total charge density is not specific enough to get insight into material properties. For this reason, VASP offers the possibility of creating band-decomposed charge densities. Selecting a specific band index or k point can shed light, e.g., on the localization of defects. This feature is helpful in computing the charge density in the vicinity of the Fermi energy. At a surface, this density is a good first approximation to compare to experimental scanning-tunneling-microscopy (STM) images.
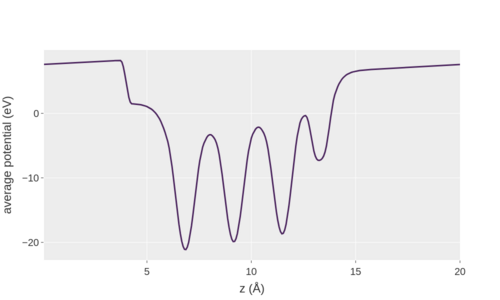
During the electronic optimization, VASP also computes the total potential. If you want to analyze the potential, use the WRT_POTENTIAL tag to select the potential that should be written. Alternatively, use the legacy tag LVTOT if you only need the total potential. A common application is to inspect planar averages parallel to surfaces or interfaces. VASP will compute these averages automatically depending on the IDIPOL setting. Compute the difference of the average potential and the Fermi energy to get the work function.
Subcategories
This category has the following 7 subcategories, out of 7 total.
Pages in category "Electronic ground-state properties"
The following 13 pages are in this category, out of 13 total.