Biased molecular dynamics: Difference between revisions
No edit summary |
No edit summary |
||
| Line 46: | Line 46: | ||
*Harmonic | *sum of Harmonic potentials (see curve (a) on the plot above) | ||
:<math> | :<math> | ||
\tilde{V}(\xi_1,\dots,\xi_{M_8}) = \sum_{\mu=1}^{M}\frac{1}{2}\kappa_{\mu} (\xi_{\mu}(q)-\xi_{0,\mu})^2 \; | \tilde{V}(\xi_1,\dots,\xi_{M_8}) = \sum_{\mu=1}^{M}\frac{1}{2}\kappa_{\mu} (\xi_{\mu}(q)-\xi_{0,\mu})^2 \; | ||
| Line 56: | Line 56: | ||
This form of bias potential is employed in several simulation protocols, such as the umbrella sampling<ref name="Torrie77"/>, umbrella integration, or steered MD, and is useful also in cases where the <math>\xi_{\mu}</math> values need restrained. | This form of bias potential is employed in several simulation protocols, such as the umbrella sampling<ref name="Torrie77"/>, umbrella integration, or steered MD, and is useful also in cases where the <math>\xi_{\mu}</math> values need restrained. | ||
*Fermi | *sum of Fermi-like step functions (see curve (b) on the plot above) | ||
:<math> | :<math> | ||
\tilde{V}(\xi_1,\dots,\xi_{M_4}) = \sum_{\mu=1}^{ | \tilde{V}(\xi_1,\dots,\xi_{M_4}) = \sum_{\mu=1}^{M_4}\frac{A_{\mu}}{1+\text{exp}\left [-D_{\mu}\frac{\xi(q)}{\xi_{0\mu}} -1 \right ]} \; | ||
</math> | </math> | ||
where the sum runs all (<math>M_4</math>) coordinates the potential acts upon, which are defined in the {{FILE|ICONST}}-file by setting the status to 4. | where the sum runs all (<math>M_4</math>) coordinates the potential acts upon, which are defined in the {{FILE|ICONST}}-file by setting the status to 4. | ||
The parameters of the potential, <math>A_{\mu}</math> (the height of step), <math>D_{\mu}</math> (controlling the slope around the point <math>\xi_{0 | The parameters of the potential, <math>A_{\mu}</math> (the height of step), <math>D_{\mu}</math> (controlling the slope around the point <math>\xi_{0\mu}</math>), and <math>\xi_{0\mu}</math> (position of the step), are defined, respectively, | ||
via the keywords {{TAG|FBIAS_A}}, {{TAG|FBIAS_D}}, and {{TAG|FBIAS_R0}} in {{FILE|INCAR}}. | via the keywords {{TAG|FBIAS_A}}, {{TAG|FBIAS_D}}, and {{TAG|FBIAS_R0}} in {{FILE|INCAR}}. | ||
The number of items defined via {{TAG|FBIAS_A}}, {{TAG|FBIAS_D}}, and {{TAG|FBIAS_R0}} must be equal to <math>M_4</math>, otherwise the calculation terminates with an error message. | The number of items defined via {{TAG|FBIAS_A}}, {{TAG|FBIAS_D}}, and {{TAG|FBIAS_R0}} must be equal to <math>M_4</math>, otherwise the calculation terminates with an error message. | ||
This form of potential is suitable especially for imposing restriction on the upper (or lower) limit of value of <math>\xi</math>. | This form of potential is suitable especially for imposing restriction on the upper (or lower) limit of value of <math>\xi</math>. | ||
*Gauss | *sum of Gauss functions (see curve (b) on the plot above) | ||
:<math> | :<math> | ||
\tilde{V}(\xi_1,\dots,\xi_{M}) = | \tilde{V}(\xi_1,\dots,\xi_{M}) = \sum_{\nu=1}^{N_5}h_{\nu}\text{exp}\left [-\frac{\sum_{\mu=1}^{M_5}(\xi_{\mu}(q)-\xi_{0\nu,\mu})^2}{2w_{\nu}^2} \right ], \; | ||
</math> | </math> | ||
where the | where <math>N_5</math> is the number of Gaussian functions and | ||
<math>M_5</math> is the number of coordinates the potential acts upon. | |||
The latter defined in the {{FILE|ICONST}}-file by setting the status to 5. | |||
The parameters of the potentials | |||
Revision as of 12:55, 6 April 2023
The probability density for a geometric parameter ξ of the system driven by a Hamiltonian:
- [math]\displaystyle{ H(q,p) = T(p) + V(q), \; }[/math]
with T(p), and V(q) being kinetic, and potential energies, respectively, can be written as:
- [math]\displaystyle{ P(\xi_i)=\frac{\int\delta\Big(\xi(q)-\xi_i\Big) \exp\left\{-H(q,p)/k_B\,T\right\} dq\,dp}{\int \exp\left\{-H(q,p)/k_B\,T\right\}dq\,dp} = \langle\delta\Big(\xi(q)-\xi_i\Big)\rangle_{H}. }[/math]
The term [math]\displaystyle{ \langle X \rangle_H }[/math] stands for a thermal average of quantity X evaluated for the system driven by the Hamiltonian H.
If the system is modified by adding a bias potential [math]\displaystyle{ \tilde{V}(\xi) }[/math] acting on one or multiple selected internal coordinates of the system ξ=ξ(q), the Hamiltonian takes a form:
- [math]\displaystyle{ \tilde{H}(q,p) = H(q,p) + \tilde{V}(\xi), }[/math]
and the probability density of ξ in the biased ensemble is:
- [math]\displaystyle{ \tilde{P}(\xi_i)= \frac{\int \delta\Big(\xi(q)-\xi_i\Big) \exp\left\{-\tilde{H}(q,p)/k_B\,T\right\} dq\,dp}{\int \exp\left\{-\tilde{H}(q,p)/k_B\,T\right\}dq\,dp} = \langle\delta\Big(\xi(q)-\xi_i\Big)\rangle_{\tilde{H}} }[/math]
It can be shown that the biased and unbiased averages are related via a simple formula:
- [math]\displaystyle{ P(\xi_i)=\tilde{P}(\xi_i) \frac{\exp\left\{\tilde{V}(\xi)/k_B\,T\right\}}{\langle \exp\left\{\tilde{V}(\xi)/k_B\,T\right\} \rangle_{\tilde{H}}}. }[/math]
More generally, an observable [math]\displaystyle{ \langle A \rangle_{H} }[/math]:
- [math]\displaystyle{ \langle A \rangle_{H} = \frac{\int A(q) \exp\left\{-H(q,p)/k_B\,T\right\} dq\,dp}{\int \exp\left\{-H(q,p)/k_B\,T\right\}dq\,dp} }[/math]
can be expressed in terms of thermal averages within the biased ensemble:
- [math]\displaystyle{ \langle A \rangle_{H} =\frac{\langle A(q) \,\exp\left\{\tilde{V}(\xi)/k_B\,T\right\} \rangle_{\tilde{H}}}{\langle \exp\left\{\tilde{V}(\xi)/k_B\,T\right\} \rangle_{\tilde{H}}}. }[/math]
Simulation methods such as umbrella sampling[1] use a bias potential to enhance sampling of ξ in regions with low P(ξi) such as transition regions of chemical reactions. The correct distributions are recovered afterwards using the equation for [math]\displaystyle{ \langle A \rangle_{H} }[/math] above.
A more detailed description of the method can be found in Ref.[2]. Biased molecular dynamics can be used also to introduce soft geometric constraints in which the controlled geometric parameter is not strictly constant, instead it oscillates in a narrow interval of values. The bias potentials are supported both the NVT and NpT MD simulations regardless of the particular thermostat and/or barostat setting. Different types of potentials can be freely combined.
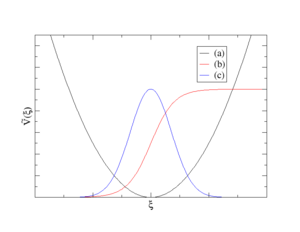
Supported types of bias potentials
Presently, the following types of bias potential are supported:
- sum of Harmonic potentials (see curve (a) on the plot above)
- [math]\displaystyle{ \tilde{V}(\xi_1,\dots,\xi_{M_8}) = \sum_{\mu=1}^{M}\frac{1}{2}\kappa_{\mu} (\xi_{\mu}(q)-\xi_{0,\mu})^2 \; }[/math]
where the sum runs all ([math]\displaystyle{ M_8 }[/math]) coordinates the potential acts upon, which are defined in the ICONST-file by setting the status to 8. The parameters of the potential, [math]\displaystyle{ \kappa_{\mu} }[/math] (force constant) and [math]\displaystyle{ \xi_{0,\mu} }[/math] (minimum of potential), are defined, respectively, via the keywords SPRING_K and SPRING_R0 in INCAR. Optionally, it is also possible to change the value of [math]\displaystyle{ \xi_{0,\mu} }[/math] every MD step at a constant rate defined via parameter SPRING_V. The number of items defined via SPRING_K, SPRING_R0, and SPRING_V must be equal to [math]\displaystyle{ M_8 }[/math], otherwise the calculation terminates with an error message. This form of bias potential is employed in several simulation protocols, such as the umbrella sampling[1], umbrella integration, or steered MD, and is useful also in cases where the [math]\displaystyle{ \xi_{\mu} }[/math] values need restrained.
- sum of Fermi-like step functions (see curve (b) on the plot above)
- [math]\displaystyle{ \tilde{V}(\xi_1,\dots,\xi_{M_4}) = \sum_{\mu=1}^{M_4}\frac{A_{\mu}}{1+\text{exp}\left [-D_{\mu}\frac{\xi(q)}{\xi_{0\mu}} -1 \right ]} \; }[/math]
where the sum runs all ([math]\displaystyle{ M_4 }[/math]) coordinates the potential acts upon, which are defined in the ICONST-file by setting the status to 4. The parameters of the potential, [math]\displaystyle{ A_{\mu} }[/math] (the height of step), [math]\displaystyle{ D_{\mu} }[/math] (controlling the slope around the point [math]\displaystyle{ \xi_{0\mu} }[/math]), and [math]\displaystyle{ \xi_{0\mu} }[/math] (position of the step), are defined, respectively, via the keywords FBIAS_A, FBIAS_D, and FBIAS_R0 in INCAR. The number of items defined via FBIAS_A, FBIAS_D, and FBIAS_R0 must be equal to [math]\displaystyle{ M_4 }[/math], otherwise the calculation terminates with an error message. This form of potential is suitable especially for imposing restriction on the upper (or lower) limit of value of [math]\displaystyle{ \xi }[/math].
- sum of Gauss functions (see curve (b) on the plot above)
- [math]\displaystyle{ \tilde{V}(\xi_1,\dots,\xi_{M}) = \sum_{\nu=1}^{N_5}h_{\nu}\text{exp}\left [-\frac{\sum_{\mu=1}^{M_5}(\xi_{\mu}(q)-\xi_{0\nu,\mu})^2}{2w_{\nu}^2} \right ], \; }[/math]
where [math]\displaystyle{ N_5 }[/math] is the number of Gaussian functions and [math]\displaystyle{ M_5 }[/math] is the number of coordinates the potential acts upon. The latter defined in the ICONST-file by setting the status to 5. The parameters of the potentials
Andersen thermostat
- For a biased molecular dynamics run with Andersen thermostat, one has to:
- Set the standard MD-related tags: IBRION=0, TEBEG, POTIM, and NSW
- Set MDALGO=1 (MDALGO=11 in VASP 5.x), and choose an appropriate setting for ANDERSEN_PROB
- In order to avoid updating of the bias potential, set HILLS_BIN=NSW
- Define collective variables in the ICONST-file, and set the STATUS parameter for the collective variables to 5
- Define the bias potential in the PENALTYPOT-file
Nose-Hoover thermostat
- For a biased molecular dynamics run with Nose-Hoover thermostat, one has to:
- Set the standard MD-related tags: IBRION=0, TEBEG, POTIM, and NSW
- Set MDALGO=2 (MDALGO=21 in VASP 5.x), and choose an appropriate setting for SMASS
- In order to avoid updating of the bias potential, set HILLS_BIN=NSW
- Define collective variables in the ICONST-file, and set the STATUS parameter for the collective variables to 5
- Define the bias potential in the PENALTYPOT-file
The values of all collective variables for each MD step are listed in the REPORT-file, check the lines after the string Metadynamics.
References
- ↑ a b G. M. Torrie and J. P. Valleau, J. Comp. Phys. 23, 187 (1977).
- ↑ D. Frenkel and B. Smit, Understanding molecular simulations: from algorithms to applications, Academic Press: San Diego, 2002.
