Wrap-around errors: Difference between revisions
No edit summary |
No edit summary |
||
| Line 2: | Line 2: | ||
Wrap around errors arise if the FFT meshes are not | Wrap around errors arise if the FFT meshes are not | ||
sufficiently large. It can be shown that no errors exist | sufficiently large. It can be shown that no errors exist | ||
if the FFT meshes contain all <math>\ | if the FFT meshes contain all <math>\mathbf{G}</math> vectors up to <math>2 G_{\rm cut}</math>. | ||
[[File:Wrap errors spheres.png|350px|thumb|Fig. 1: Sphere intersections for <math>G_{\mathrm{cut}}</math>]] | [[File:Wrap errors spheres.png|350px|thumb|Fig. 1: Sphere intersections for <math>G_{\mathrm{cut}}</math>]] | ||
| Line 13: | Line 13: | ||
<math> | <math> | ||
| \phi_{n\ | | \phi_{n\mathbf{k}} \rangle = \sum_\mathbf{G} C_{\mathbf{G}n\mathbf{k}} | \mathbf{k}+\mathbf{G}\rangle, | ||
</math> | </math> | ||
| Line 19: | Line 19: | ||
<math> | <math> | ||
\langle \ | \langle \mathbf{r}| \phi_{n\mathbf{k}} \rangle = \sum_\mathbf{G} \langle \mathbf{r}| \mathbf{k}+\mathbf{G}\rangle \langle \mathbf{k}+\mathbf{G}|\phi_{n\mathbf{k}} \rangle | ||
= \frac{1}{\Omega^{1/2}} \sum_\ | = \frac{1}{\Omega^{1/2}} \sum_\mathbf{G} e^{i(\mathbf{k}+\mathbf{G})\mathbf{r}} C_{\mathbf{G}n\mathbf{k}}. | ||
</math> | </math> | ||
| Line 26: | Line 26: | ||
<math> | <math> | ||
C_{\ | C_{\mathbf{r}n\mathbf{k}}= \sum_{\mathbf{G}} C_{\mathbf{G}n\mathbf{k}} e^{i\mathbf{G} \mathbf{r}} \qquad \qquad \qquad | ||
C_{\ | C_{\mathbf{G}n\mathbf{k}}= \frac{1}{N_{\mathrm{FFT}}} \sum_{\mathbf{r}} C_{\mathbf{r}n\mathbf{k}} e^{-i\mathbf{G} \mathbf{r}}. | ||
</math> | </math> | ||
| Line 33: | Line 33: | ||
<math> | <math> | ||
\langle\ | \langle\mathbf{r}| \phi_{n\mathbf{k}} \rangle = \phi_{n\mathbf{k}}(r) = \frac{1}{\Omega^{1/2}} C_{\mathbf{r}n\mathbf{k}} e^{i\mathbf{k}\mathbf{r}}. | ||
</math> | </math> | ||
| Line 39: | Line 39: | ||
<math> | <math> | ||
\rho^{\mathrm{ps}}_{\ | \rho^{\mathrm{ps}}_{\mathbf{r}} \equiv \langle \mathbf{r} |\rho^{\mathrm{ps}} | \mathbf{r} \rangle = | ||
\sum_\ | \sum_\mathbf{k} w_{\mathbf{k}} \sum_n f_{n\mathbf{k}} \phi_{n\mathbf{k}}(r) \phi^{*}_{n\mathbf{k}}(r) , | ||
</math> | </math> | ||
| Line 46: | Line 46: | ||
<math> | <math> | ||
\rho^{\mathrm{ps}}_\ | \rho^{\mathrm{ps}}_\mathbf{G} \equiv | ||
\frac{1}{\Omega} \int \langle\ | \frac{1}{\Omega} \int \langle\mathbf{r} | \rho^{\mathrm{ps}}| \mathbf{r}\rangle e^{-i \mathbf{G}\mathbf{r}}\, d \mathbf{r} \to \frac{1}{N_{\mathrm{FFT}}} \sum_{\mathbf{r}} \rho^{\mathrm{ps}}_{\mathbf{r}} e^{-i \mathbf{G}\mathbf{r}}. | ||
</math> | </math> | ||
Using the above equations for <math>\rho^{\mathrm{ps}}_{\ | Using the above equations for <math>\rho^{\mathrm{ps}}_{\mathbf{r}}</math> and <math>C_{\mathbf{r}n\mathbf{k}}</math> it | ||
is very easy to show that <math>\rho^{\mathrm{ps}}_{\ | is very easy to show that <math>\rho^{\mathrm{ps}}_{\mathbf{r}}</math> contains Fourier-components up | ||
to <math>2 G_{\mathrm{cut}}</math>. | to <math>2 G_{\mathrm{cut}}</math>. | ||
| Line 65: | Line 65: | ||
<math> | <math> | ||
a_{\ | a_{\mathbf{r}} = V_{\mathbf{r}} C_{\mathbf{r}n\mathbf{k}}. | ||
</math> | </math> | ||
Only the components <math>a_{\ | Only the components <math>a_{\mathbf{G}}</math> with <math>|\mathbf{G}| < G_{\mathrm{cut}}</math> are taken into | ||
account (see section {{TAG|ALGO}}: <math>a_{\ | account (see section {{TAG|ALGO}}: <math>a_{\mathbf{G}}</math> is added to the wavefunction | ||
during the iterative refinement of the wavefunctions <math>C_{\ | during the iterative refinement of the wavefunctions <math>C_{\mathbf{G}n\mathbf{k}}</math>, | ||
and <math>C_{\ | and <math>C_{\mathbf{G}n\mathbf{k}}</math> contains only components up to <math>G_{\mathrm{cut}}</math>). | ||
From the previous theorem we see that <math>a_{\ | From the previous theorem we see that <math>a_{\mathbf{r}}</math> contains | ||
components up to <math>3 G_{\mathrm{cut}}</math> (<math>V_{\ | components up to <math>3 G_{\mathrm{cut}}</math> (<math>V_{\mathbf{r}}</math> contains components up to | ||
<math>2 G_{\mathrm{cut}}</math>). | <math>2 G_{\mathrm{cut}}</math>). | ||
| Line 82: | Line 82: | ||
the acceleration <math>a</math> components up to <math>3 G_{\mathrm{cut}}</math>, which are reflected | the acceleration <math>a</math> components up to <math>3 G_{\mathrm{cut}}</math>, which are reflected | ||
in (third sphere) because of the finite size of the FFT-mesh. Nevertheless | in (third sphere) because of the finite size of the FFT-mesh. Nevertheless | ||
the components <math>a_{\ | the components <math>a_{\mathbf{G}}</math> with <math>| \mathbf{G}| < G_{\mathrm{cut}}</math> are correct i.e. | ||
the small sphere does not intersect with the third large sphere} | the small sphere does not intersect with the third large sphere} | ||
---- | ---- | ||
[[Category:Electronic minimization]][[Category:Charge density]][[Category:Theory]] | [[Category:Electronic minimization]][[Category:Charge density]][[Category:Theory]] | ||
Revision as of 08:36, 14 October 2025
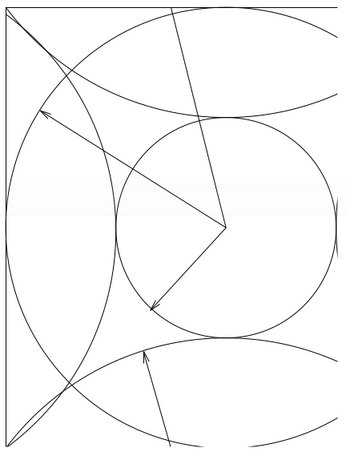
In this section we will discuss wrap around errors. Wrap around errors arise if the FFT meshes are not sufficiently large. It can be shown that no errors exist if the FFT meshes contain all [math]\displaystyle{ \mathbf{G} }[/math] vectors up to [math]\displaystyle{ 2 G_{\rm cut} }[/math].
It can be shown that the charge density contains components up to [math]\displaystyle{ 2 G_{\mathrm{cut}} }[/math], where [math]\displaystyle{ 2 G_{\mathrm{cut}} }[/math] is the "longest" plane wave in the basis set:
The wavefunction is defined as
[math]\displaystyle{ | \phi_{n\mathbf{k}} \rangle = \sum_\mathbf{G} C_{\mathbf{G}n\mathbf{k}} | \mathbf{k}+\mathbf{G}\rangle, }[/math]
and in real space it is given by
[math]\displaystyle{ \langle \mathbf{r}| \phi_{n\mathbf{k}} \rangle = \sum_\mathbf{G} \langle \mathbf{r}| \mathbf{k}+\mathbf{G}\rangle \langle \mathbf{k}+\mathbf{G}|\phi_{n\mathbf{k}} \rangle = \frac{1}{\Omega^{1/2}} \sum_\mathbf{G} e^{i(\mathbf{k}+\mathbf{G})\mathbf{r}} C_{\mathbf{G}n\mathbf{k}}. }[/math]
Using Fast Fourier transformations one can define
[math]\displaystyle{ C_{\mathbf{r}n\mathbf{k}}= \sum_{\mathbf{G}} C_{\mathbf{G}n\mathbf{k}} e^{i\mathbf{G} \mathbf{r}} \qquad \qquad \qquad C_{\mathbf{G}n\mathbf{k}}= \frac{1}{N_{\mathrm{FFT}}} \sum_{\mathbf{r}} C_{\mathbf{r}n\mathbf{k}} e^{-i\mathbf{G} \mathbf{r}}. }[/math]
Therefore the wavefunction can be written in real space as
[math]\displaystyle{ \langle\mathbf{r}| \phi_{n\mathbf{k}} \rangle = \phi_{n\mathbf{k}}(r) = \frac{1}{\Omega^{1/2}} C_{\mathbf{r}n\mathbf{k}} e^{i\mathbf{k}\mathbf{r}}. }[/math]
The charge density is simply given by
[math]\displaystyle{ \rho^{\mathrm{ps}}_{\mathbf{r}} \equiv \langle \mathbf{r} |\rho^{\mathrm{ps}} | \mathbf{r} \rangle = \sum_\mathbf{k} w_{\mathbf{k}} \sum_n f_{n\mathbf{k}} \phi_{n\mathbf{k}}(r) \phi^{*}_{n\mathbf{k}}(r) , }[/math]
and in the reciprocal mesh it can be written as
[math]\displaystyle{ \rho^{\mathrm{ps}}_\mathbf{G} \equiv \frac{1}{\Omega} \int \langle\mathbf{r} | \rho^{\mathrm{ps}}| \mathbf{r}\rangle e^{-i \mathbf{G}\mathbf{r}}\, d \mathbf{r} \to \frac{1}{N_{\mathrm{FFT}}} \sum_{\mathbf{r}} \rho^{\mathrm{ps}}_{\mathbf{r}} e^{-i \mathbf{G}\mathbf{r}}. }[/math]
Using the above equations for [math]\displaystyle{ \rho^{\mathrm{ps}}_{\mathbf{r}} }[/math] and [math]\displaystyle{ C_{\mathbf{r}n\mathbf{k}} }[/math] it is very easy to show that [math]\displaystyle{ \rho^{\mathrm{ps}}_{\mathbf{r}} }[/math] contains Fourier-components up to [math]\displaystyle{ 2 G_{\mathrm{cut}} }[/math].
Generally it can be shown that a the convolution [math]\displaystyle{ f_r=f^1_r f^2_r }[/math] of two functions [math]\displaystyle{ f^1_r }[/math] with Fourier-components up to [math]\displaystyle{ G_1 }[/math] and [math]\displaystyle{ f^2_r }[/math] with Fourier-components up to [math]\displaystyle{ G_2 }[/math] contains Fourier-components up to [math]\displaystyle{ G_1+G_2 }[/math].
The property of the convolution comes once again into play, when the action of the Hamiltonian onto a wavefunction is calculated. The action of the local-potential is given by
[math]\displaystyle{ a_{\mathbf{r}} = V_{\mathbf{r}} C_{\mathbf{r}n\mathbf{k}}. }[/math]
Only the components [math]\displaystyle{ a_{\mathbf{G}} }[/math] with [math]\displaystyle{ |\mathbf{G}| \lt G_{\mathrm{cut}} }[/math] are taken into account (see section ALGO: [math]\displaystyle{ a_{\mathbf{G}} }[/math] is added to the wavefunction during the iterative refinement of the wavefunctions [math]\displaystyle{ C_{\mathbf{G}n\mathbf{k}} }[/math], and [math]\displaystyle{ C_{\mathbf{G}n\mathbf{k}} }[/math] contains only components up to [math]\displaystyle{ G_{\mathrm{cut}} }[/math]). From the previous theorem we see that [math]\displaystyle{ a_{\mathbf{r}} }[/math] contains components up to [math]\displaystyle{ 3 G_{\mathrm{cut}} }[/math] ([math]\displaystyle{ V_{\mathbf{r}} }[/math] contains components up to [math]\displaystyle{ 2 G_{\mathrm{cut}} }[/math]).
If the FFT-mesh contains all components up to [math]\displaystyle{ 2 G_{\mathrm cut} }[/math] the resulting wrap-around error is once again 0. This can be easily seen in Fig. 1. Here we see that the small sphere contains all plane waves included in the basis set [math]\displaystyle{ G\lt G_{\mathrm{cut}} }[/math]. The charge density contains components up to [math]\displaystyle{ 2 G_{\mathrm{cut}} }[/math] (second sphere), and the acceleration [math]\displaystyle{ a }[/math] components up to [math]\displaystyle{ 3 G_{\mathrm{cut}} }[/math], which are reflected in (third sphere) because of the finite size of the FFT-mesh. Nevertheless the components [math]\displaystyle{ a_{\mathbf{G}} }[/math] with [math]\displaystyle{ | \mathbf{G}| \lt G_{\mathrm{cut}} }[/math] are correct i.e. the small sphere does not intersect with the third large sphere}
