Delta self-consistent field

[math]\displaystyle{ \Delta }[/math]SCF is a method that allows to calculate energies of neutral excitation within DFT by constraining occupations. Within the Franck-Condon approximation, the electronic excitation is much faster than the nuclear motion. Thus, [math]\displaystyle{ \Delta }[/math]SCF can be used for calculating excited-state properties such as vertical absorption (VAE) and vertical emission energy (VEE). Furthermore, this method can be used to calculate the zero-phonon lines (ZPL) by performing a full atomic relaxation in the excited-state configuration and thus account for the Stockes shifts. This method is commonly used for calculating the optical properties of point defects in semiconductors and insulators .

Vertical absorption energies (VAE)

Schematic representation of the excitation energies.

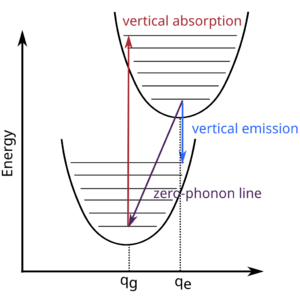
The VAE can be calculated by performing a full SCF calculation of the system in its excited-state configuration following three steps:

1. Perform a ground state calculation to obtain the total energy of the system in its ground state configuration, [math]\displaystyle{ E_{gs} }[/math].
2. Set the occupations of the Kohn-Sham states to represent the excited via FERWE and FERDO tags. Then, perform a full SCF calculation to obtain the total energy of the system in its excited-state configuration, [math]\displaystyle{ E_{ex} }[/math].
3. The VAE is then given by the difference between the total energies of the excited and ground states: [math]\displaystyle{ \mathrm{VEE} = E_{ex} - E_{gs}. }[/math]

Zero-phonon lines (ZPL)

The ZPL calculation requires performing a full atomic relaxation in the excited state configuration. The ZPL calculation can be performed in three steps:

1. Perform a ground state calculation to obtain the total energy of the system in its ground state configuration, [math]\displaystyle{ E_gs }[/math].
2. Set the occupations of the Kohn-Sham states to represent the excited via FERWE and FERDO tags. Then, perform a full atomic relaxation to obtain the total energy of the system in its relaxed excited-state configuration, [math]\displaystyle{ E_{ex}^* }[/math]
3. The ZPL is then given by the difference between the total energies of the relaxed excited and ground states: [math]\displaystyle{ \mathrm{ZPL} = E_{ex}^* - E_{gs} }[/math]

Vertical emission energies (VEE)

The VEE calculation can be performed in three steps:

1. Set the occupations of the bands to represent the excited state via FERWE and FERDO tags. Perform a full atomic relaxation of the excited state to obtain the total energy [math]\displaystyle{ E_{ex} }[/math].
2. Remove the occupation constraints and perform a full SCF calculation to obtain the total energy of the system in this atomic configuration, [math]\displaystyle{ E_{gs}^* }[/math].
3. The VEE is then given by the difference between the total energies of the excited and ground states: [math]\displaystyle{ \mathrm{VEE} = E_{ex} - E_{gs}^*. }[/math]

Electronic minimization

Scheme of how states order might change upon SCF calculation of the excited state.

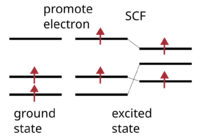
When using constrained occupation calculations, it is important to ensure that the order of the states is preserved throughout the calculation. This can be achieved by setting LDIAG=.FALSE. in ALGO=Damped or ALGO=All.

To improve convergence, it is recommended to restart the calculation from the converged WAVECAR.

Mind: ALGO=Normal,Fast,VeryFast are not recommended for constrained occupation calculations as they may lead to state reordering.

Warning: In versions of VASP between VASP 5.4.1 and VASP 6.4, the LDIAG=.FALSE. was broken and did not preserve the order of states between ionic iterations.

Example: ZPL of [math]\displaystyle{ NV^- }[/math] center in diamond

[math]\displaystyle{ NV^- }[/math] center in 64-atom diamond supercell.

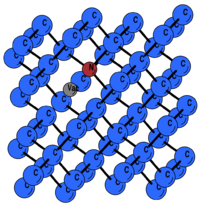
We consider a negatively charged point defect in diamond, so called [math]\displaystyle{ NV^- }[/math] which consist of a N substitution and a vacancy. This is a well studied point defect in diamond which can be used here for illustrating the principle of the ZPL calculations . In this example, we consider a single [math]\displaystyle{ NV^- }[/math] in a 64-atom supercell.

1. Perform a full atomic relaxation of the [math]\displaystyle{ NV^- }[/math] center in its ground state. Identify the band index of the states involved in the excitation.

            Spin up                             Spin down
   ...
   124       8.8280      1.00000         124       8.9642      1.00000
   125       8.8280      1.00000         125       8.9642      1.00000
   126      10.1514      1.00000         126      10.5683      1.00000
   127      11.1936      1.00000         127      12.4369      0.00000
   128      11.1936      1.00000         128      12.4369      0.00000
   129      13.6991      0.00000         129      13.7261      0.00000
   ...

To simulate the excitation we promote an electron from the highest occupied state in the spin-down channel (126) to the lowest unoccupied state in the same channel (127). Thus, we need to provide the following occupations:

FERWE = 128*1 64*0
FERDO = 125*1 1*0 1*1 65*0

Here, the first number is a multiplicity and the second number is the occupation, e.g., 128*1 means that the first 128 states are fully occupied. The occupations must be provided for all NBANDS and all k-points. Thus, for a 4x4x4 k-point mesh with 13 k-points in IBZ, we have:

FERWE = 128*1 64*0 128*1 64*0 128*1 64*0 128*1 64*0 128*1 64*0 128*1 64*0 128*1 64*0 128*1 64*0 128*1 64*0 128*1 64*0 128*1 64*0 128*1 64*0 128*1 64*0
FERDO = 125*1 1*0 1*1 65*0 125*1 1*0 1*1 65*0 125*1 1*0 1*1 65*0 125*1 1*0 1*1 65*0 125*1 1*0 1*1 65*0 125*1 1*0 1*1 65*0 125*1 1*0 1*1 65*0 125*1 1*0 1*1 65*0 125*1 1*0 1*1 65*0 125*1 1*0 1*1 65*0 125*1 1*0 1*1 65*0 125*1 1*0 1*1 65*0 125*1 1*0 1*1 65*0

2. Perform a full SCF calculation with the above occupations to obtain the total energy of the system in its excited-state configuration, [math]\displaystyle{ E_{ex} }[/math]. Make sure that the correct excited state is preserved throughout the calculation.

             Spin up                             Spin down
    ...
    124       8.8622      1.00000         124       8.9647      1.00000
    125       8.8622      1.00000         125       8.9647      1.00000
    126       9.9201      1.00000         126      10.4995      0.00000
    127      11.4574      1.00000         127      12.4388      1.00000
    128      11.4574      1.00000         128      12.4388      0.00000
    129      13.6252      0.00000         129      13.6705      0.00000
    ...

By subtracting the ground-state energy from the excited state we find the VAE of 1.77 eV.

3. To calculate ZPL, perform a full atomic relaxation of this excited state. After the convergence was achieved make sure that the excited state was presevred and the converged configuration is correct.

             Spin up                             Spin down
    ...
    124       8.8276      1.00000         124       8.9334      1.00000
    125       8.8276      1.00000         125       8.9334      1.00000
    126      10.0760      1.00000         126      10.7072      0.00000
    127      11.3836      1.00000         127      12.3573      1.00000
    128      11.3836      1.00000         128      12.3573      0.00000
    129      13.5935      0.00000         129      13.6348      0.00000
    ...

The total energy difference between the ground state and the excited state after the ionic relaxation, i.e., ZPL is 1.59 eV.