Delta self-consistent field: Difference between revisions
No edit summary |
No edit summary |
||
| Line 10: | Line 10: | ||
=== Step 2 === | === Step 2 === | ||
Set the [[:Category:Electronic occupancy|occupations of the Kohn-Sham states]] to represent the excited via {{TAG|FERWE}} and {{TAG|FERDO}} tags. Then, perform a full SCF calculation to obtain the total energy of the system in its excited-state configuration, <math display="inline">E_{ex}</math>. | Set the [[:Category:Electronic occupancy|occupations of the Kohn-Sham states]] to represent the excited via {{TAG|FERWE}} and {{TAG|FERDO}} tags. Then, perform a full [[#Electronic minimization with constrained electronic occupation|SCF calculation with constrained electronic occupancies]] to obtain the total energy of the system in its excited-state configuration, <math display="inline">E_{ex}</math>. | ||
=== Step 3 === | === Step 3 === | ||
| Line 18: | Line 18: | ||
The ZPL calculation requires performing a full atomic relaxation in the excited | The ZPL calculation requires performing a full atomic relaxation in the excited | ||
state configuration. The ZPL calculation can be performed in three steps: | state configuration. The ZPL calculation can be performed in three steps: | ||
=== Step 1 === | |||
Perform a [[Setting up an electronic minimization|ground-state calculation]] to obtain the total energy of the system in its ground-state configuration, <math display="inline">E_{gs}</math>. | |||
=== Step 2 === | |||
Set the [[:Category:Electronic occupancy|occupations of the Kohn-Sham states]] to represent the excited via {{TAG|FERWE}} and {{TAG|FERDO}} tags, i.e. set up a [[#Electronic minimization with constrained electronic occupation|constrained occupation calculation]]. Then, perform a full [[Structure optimization|atomic relaxation]] to obtain the total energy of the system in its excited-state configuration at relaxed atomic positions, <math display="inline">E_{ex}^*</math> | |||
=== Step 3 === | |||
The ZPL is then given by the difference between the total energies of the relaxed excited and ground states: <math display="inline">\mathrm{ZPL} = E_{ex}^* - E_{gs}</math> | |||
== Vertical emission energies (VEE) == | == Vertical emission energies (VEE) == | ||
The VEE calculation can be performed in three steps: | The VEE calculation can be performed in three steps: | ||
== Electronic minimization == | === Step 1 === | ||
Set the occupations of the bands to represent the excited state via {{TAG|FERWE}} and {{TAG|FERDO}} tags. Perform a full [[Structure optimization|atomic relaxation]] of the excited state to obtain the total energy <math>E_{ex}</math>. | |||
=== Step 2 === | |||
Remove the occupation constraints and perform a full SCF calculation to obtain the total energy of the system in this atomic configuration, <math display="inline">E_{gs}^*</math>. | |||
=== Step 3 === | |||
The VEE is then given by the difference between the total energies of the excited and ground states: <math display="inline">\mathrm{VEE} = E_{ex} - E_{gs}^*.</math> | |||
== Electronic minimization with constrained electronic occupation == | |||
[[Image:Diagram_delta_scf.png|200px|thumb|Scheme of how states order might change upon SCF calculation of the excited state.]] | [[Image:Diagram_delta_scf.png|200px|thumb|Scheme of how states order might change upon SCF calculation of the excited state.]] | ||
When using constrained occupation calculations, it is important to ensure that the order of the states is preserved throughout the calculation. This can be achieved by setting {{TAG|LDIAG}}=.FALSE. in {{TAG|ALGO}}=Damped or {{TAG|ALGO}}=All. | When using constrained occupation calculations, it is important to ensure that the order of the states is preserved throughout the calculation. This can be achieved by setting {{TAG|LDIAG}}=.FALSE. in {{TAG|ALGO}}=Damped or {{TAG|ALGO}}=All. | ||
| Line 39: | Line 51: | ||
[[Image:Diamond_nv.png|200px|thumb|<math display="inline">\mathrm{NV}^-</math> center in | [[Image:Diamond_nv.png|200px|thumb|<math display="inline">\mathrm{NV}^-</math> center in | ||
64-atom diamond supercell.]] | 64-atom diamond supercell.]] | ||
We consider a negatively charged point defect in diamond, so called | We consider a negatively charged point defect in diamond, so-called <math display="inline">\mathrm{NV}^-</math>, which consists of an N substitution and a vacancy. This is a well-studied point defect in diamond, which can be used here for illustrating the principle of the ZPL calculations {{cite|Lofgren2018}}. | ||
In this example, we consider a single <math display="inline">\mathrm{NV}^-</math> in a 64-atom supercell. | In this example, we consider a single <math display="inline">\mathrm{NV}^-</math> in a 64-atom supercell. | ||
=== Step 1 === | === Step 1 === | ||
Perform a full atomic relaxation of the <math display="inline">\mathrm{NV}^-</math> center in its ground state. | Perform a full [[Structure optimization|atomic relaxation]] of the <math display="inline">\mathrm{NV}^-</math> center in its ground state. | ||
Identify the band index of the states involved in the excitation. | Identify the band index of the states involved in the excitation. | ||
| Line 56: | Line 68: | ||
... | ... | ||
To simulate the excitation we promote an electron from the highest occupied state in the spin-down channel (126) to the lowest unoccupied state in the same channel (127). Thus, we need to provide the following occupations: | To simulate the excitation, we promote an electron from the highest occupied state in the spin-down channel (126) to the lowest unoccupied state in the same channel (127). Thus, we need to provide the following occupations: | ||
{{TAG|FERWE}} = 128*1 64*0 | {{TAG|FERWE}} = 128*1 64*0 | ||
| Line 79: | Line 91: | ||
... | ... | ||
By subtracting the ground-state energy from the excited state we find the VAE of 1.77 eV. | By subtracting the ground-state energy from the excited state, we find the VAE of 1.77 eV. | ||
=== Step 3 === | === Step 3 === | ||
To calculate ZPL, perform a full atomic relaxation of this excited state. After the convergence was achieved make sure that the excited state was | To calculate ZPL, perform a full atomic relaxation of this excited state. After the convergence was achieved, make sure that the excited state was preserved and the converged configuration is correct. | ||
Spin up Spin down | Spin up Spin down | ||
... | ... | ||
Revision as of 10:08, 17 October 2025
[math]\displaystyle{ \Delta }[/math]SCF is a method that allows to calculate energies of neutral excitation within DFT by constraining occupations. Within the Franck-Condon approximation, the electronic excitation is much faster than the nuclear motion. Thus, [math]\displaystyle{ \Delta }[/math]SCF can be used for calculating excited-state properties such as vertical absorption (VAE) and vertical emission energy (VEE). Furthermore, this method can be used to calculate the zero-phonon lines (ZPL) by performing a full atomic relaxation in the excited-state configuration and thus account for the Stockes shifts. This method is commonly used for calculating the optical properties of point defects in semiconductors and insulators [1].
Vertical absorption energies (VAE)
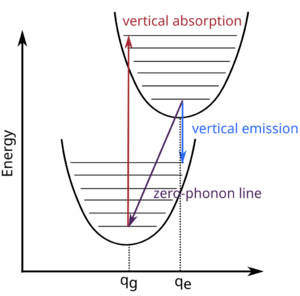
The VAE can be calculated by performing a full SCF calculation of the system in its excited-state configuration following three steps:
Step 1
Perform a ground-state calculation to obtain the total energy of the system in its ground-state configuration, [math]\displaystyle{ E_{gs} }[/math].
Step 2
Set the occupations of the Kohn-Sham states to represent the excited via FERWE and FERDO tags. Then, perform a full SCF calculation with constrained electronic occupancies to obtain the total energy of the system in its excited-state configuration, [math]\displaystyle{ E_{ex} }[/math].
Step 3
The VAE is then given by the difference between the total energies of the excited and ground states: [math]\displaystyle{ \mathrm{VEE} = E_{ex} - E_{gs}. }[/math]
Zero-phonon lines (ZPL)
The ZPL calculation requires performing a full atomic relaxation in the excited state configuration. The ZPL calculation can be performed in three steps:
Step 1
Perform a ground-state calculation to obtain the total energy of the system in its ground-state configuration, [math]\displaystyle{ E_{gs} }[/math].
Step 2
Set the occupations of the Kohn-Sham states to represent the excited via FERWE and FERDO tags, i.e. set up a constrained occupation calculation. Then, perform a full atomic relaxation to obtain the total energy of the system in its excited-state configuration at relaxed atomic positions, [math]\displaystyle{ E_{ex}^* }[/math]
Step 3
The ZPL is then given by the difference between the total energies of the relaxed excited and ground states: [math]\displaystyle{ \mathrm{ZPL} = E_{ex}^* - E_{gs} }[/math]
Vertical emission energies (VEE)
The VEE calculation can be performed in three steps:
Step 1
Set the occupations of the bands to represent the excited state via FERWE and FERDO tags. Perform a full atomic relaxation of the excited state to obtain the total energy [math]\displaystyle{ E_{ex} }[/math].
Step 2
Remove the occupation constraints and perform a full SCF calculation to obtain the total energy of the system in this atomic configuration, [math]\displaystyle{ E_{gs}^* }[/math].
Step 3
The VEE is then given by the difference between the total energies of the excited and ground states: [math]\displaystyle{ \mathrm{VEE} = E_{ex} - E_{gs}^*. }[/math]
Electronic minimization with constrained electronic occupation
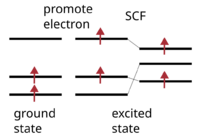
When using constrained occupation calculations, it is important to ensure that the order of the states is preserved throughout the calculation. This can be achieved by setting LDIAG=.FALSE. in ALGO=Damped or ALGO=All.
To improve convergence, it is recommended to restart the calculation from the converged WAVECAR.
| Mind: ALGO=Normal,Fast,VeryFast are not recommended for constrained occupation calculations as they may lead to state reordering. |
| Warning: In versions of VASP between VASP 5.4.1 and VASP 6.4, the LDIAG=.FALSE. was broken and did not preserve the order of states between ionic iterations. |
Example: ZPL of [math]\displaystyle{ \mathrm{NV}^- }[/math] center in diamond
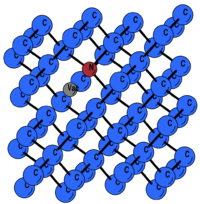
We consider a negatively charged point defect in diamond, so-called [math]\displaystyle{ \mathrm{NV}^- }[/math], which consists of an N substitution and a vacancy. This is a well-studied point defect in diamond, which can be used here for illustrating the principle of the ZPL calculations [2]. In this example, we consider a single [math]\displaystyle{ \mathrm{NV}^- }[/math] in a 64-atom supercell.
Step 1
Perform a full atomic relaxation of the [math]\displaystyle{ \mathrm{NV}^- }[/math] center in its ground state. Identify the band index of the states involved in the excitation.
Spin up Spin down ... 124 8.8280 1.00000 124 8.9642 1.00000 125 8.8280 1.00000 125 8.9642 1.00000 126 10.1514 1.00000 126 10.5683 1.00000 127 11.1936 1.00000 127 12.4369 0.00000 128 11.1936 1.00000 128 12.4369 0.00000 129 13.6991 0.00000 129 13.7261 0.00000 ...
To simulate the excitation, we promote an electron from the highest occupied state in the spin-down channel (126) to the lowest unoccupied state in the same channel (127). Thus, we need to provide the following occupations:
FERWE = 128*1 64*0 FERDO = 125*1 1*0 1*1 65*0
Here, the first number is a multiplicity and the second number is the occupation, e.g., 128*1 means that the first 128 states are fully occupied. The occupations must be provided for all NBANDS and all k-points. Thus, for a 4x4x4 k-point mesh with 13 k-points in IBZ, we have:
FERWE = 128*1 64*0 128*1 64*0 128*1 64*0 128*1 64*0 128*1 64*0 128*1 64*0 128*1 64*0 128*1 64*0 128*1 64*0 128*1 64*0 128*1 64*0 128*1 64*0 128*1 64*0 FERDO = 125*1 1*0 1*1 65*0 125*1 1*0 1*1 65*0 125*1 1*0 1*1 65*0 125*1 1*0 1*1 65*0 125*1 1*0 1*1 65*0 125*1 1*0 1*1 65*0 125*1 1*0 1*1 65*0 125*1 1*0 1*1 65*0 125*1 1*0 1*1 65*0 125*1 1*0 1*1 65*0 125*1 1*0 1*1 65*0 125*1 1*0 1*1 65*0 125*1 1*0 1*1 65*0
Step 2
Perform a full SCF calculation with the above occupations to obtain the total energy of the system in its excited-state configuration, [math]\displaystyle{ E_{ex} }[/math]. Make sure that the correct excited state is preserved throughout the calculation.
Spin up Spin down
...
124 8.8622 1.00000 124 8.9647 1.00000
125 8.8622 1.00000 125 8.9647 1.00000
126 9.9201 1.00000 126 10.4995 0.00000
127 11.4574 1.00000 127 12.4388 1.00000
128 11.4574 1.00000 128 12.4388 0.00000
129 13.6252 0.00000 129 13.6705 0.00000
...
By subtracting the ground-state energy from the excited state, we find the VAE of 1.77 eV.
Step 3
To calculate ZPL, perform a full atomic relaxation of this excited state. After the convergence was achieved, make sure that the excited state was preserved and the converged configuration is correct.
Spin up Spin down
...
124 8.8276 1.00000 124 8.9334 1.00000
125 8.8276 1.00000 125 8.9334 1.00000
126 10.0760 1.00000 126 10.7072 0.00000
127 11.3836 1.00000 127 12.3573 1.00000
128 11.3836 1.00000 128 12.3573 0.00000
129 13.5935 0.00000 129 13.6348 0.00000
...
The total energy difference between the ground state and the excited state after the ionic relaxation, i.e., ZPL is 1.59 eV.
