Spin spirals: Difference between revisions
Vaspmaster (talk | contribs) |
Vaspmaster (talk | contribs) |
||
| Line 12: | Line 12: | ||
0 & e^{+i\bf q \cdot \bf R / 2} \end{array}\right) \left[ | 0 & e^{+i\bf q \cdot \bf R / 2} \end{array}\right) \left[ | ||
\begin{array}{c} \Psi^{\uparrow}_{\bf k}(\bf r-R) \\ | \begin{array}{c} \Psi^{\uparrow}_{\bf k}(\bf r-R) \\ | ||
\Psi^{\downarrow}_{\bf k}(\bf r-R) \end{array} \right] | \Psi^{\downarrow}_{\bf k}(\bf r-R) \end{array} \right], | ||
</math> | </math> | ||
</span> | </span> | ||
''i.e.'', from one unit cell to the next the up-spinor and down-spinors pick up an additional phase factor of <math>\exp(-i{\bf q}\cdot {\bf R}/2)</math> and <math>\exp(-i{\bf q}\cdot {\bf R}/2)</math>, respectively. | |||
The above definition gives rise to the following magnetization density: | The above definition gives rise to the following magnetization density: | ||
Revision as of 12:31, 6 July 2018
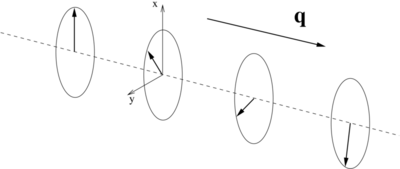
Generalized Bloch condition
Spin spirals may be conveniently modeled using a generalisation of the Bloch condition:
i.e., from one unit cell to the next the up-spinor and down-spinors pick up an additional phase factor of and , respectively.
The above definition gives rise to the following magnetization density: