Spin spirals: Difference between revisions
Vaspmaster (talk | contribs) No edit summary |
Vaspmaster (talk | contribs) |
||
| Line 17: | Line 17: | ||
''i.e.'', from one unit cell to the next the up-spinor and down-spinors pick up an additional phase factor of <math>\exp(-i{\bf q}\cdot {\bf R}/2)</math> and <math>\exp(-i{\bf q}\cdot {\bf R}/2)</math>, respectively. | ''i.e.'', from one unit cell to the next the up-spinor and down-spinors pick up an additional phase factor of <math>\exp(-i{\bf q}\cdot {\bf R}/2)</math> and <math>\exp(-i{\bf q}\cdot {\bf R}/2)</math>, respectively. | ||
Here, '''R''' is a lattice vector of the crystalline lattice, and '''q''' is the so-called spin-spiral propagation vector. | |||
The latter is commonly chosen to lie within the first Brillouin zone of the reciprocal space lattice. | |||
This condition gives rise to the following behaviour of the magnetization density: | This condition gives rise to the following behaviour of the magnetization density: | ||
| Line 31: | Line 33: | ||
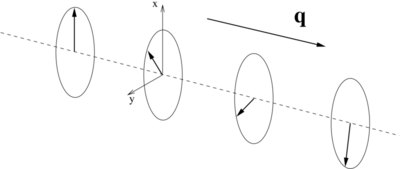
This is schematically depicted in the figure at the top of this page: | This is schematically depicted in the figure at the top of this page: | ||
the components of the magnization in the ''xy''-plane rotate about the | the components of the magnization in the ''xy''-plane rotate about the spin-spiral propagation vector '''q'''. | ||
Revision as of 12:43, 6 July 2018
Generalized Bloch condition
Spin spirals may be conveniently modeled using a generalisation of the Bloch condition:
- [math]\displaystyle{ \left[ \begin{array}{c} \Psi^{\uparrow}_{\bf k}(\bf r) \\ \Psi^{\downarrow}_{\bf k}(\bf r) \end{array} \right] = \left( \begin{array}{cc} e^{-i\bf q \cdot \bf R / 2} & 0\\ 0 & e^{+i\bf q \cdot \bf R / 2} \end{array}\right) \left[ \begin{array}{c} \Psi^{\uparrow}_{\bf k}(\bf r-R) \\ \Psi^{\downarrow}_{\bf k}(\bf r-R) \end{array} \right], }[/math]
i.e., from one unit cell to the next the up-spinor and down-spinors pick up an additional phase factor of [math]\displaystyle{ \exp(-i{\bf q}\cdot {\bf R}/2) }[/math] and [math]\displaystyle{ \exp(-i{\bf q}\cdot {\bf R}/2) }[/math], respectively. Here, R is a lattice vector of the crystalline lattice, and q is the so-called spin-spiral propagation vector. The latter is commonly chosen to lie within the first Brillouin zone of the reciprocal space lattice.
This condition gives rise to the following behaviour of the magnetization density:
- [math]\displaystyle{ {\bf m} ({\bf r} + {\bf R})= \left( \begin{array}{c} m_x({\bf r}) \cos({\bf q} \cdot {\bf R}) - m_y({\bf r}) \sin({\bf q} \cdot {\bf R}) \\ m_x({\bf r}) \sin({\bf q} \cdot {\bf R}) + m_y({\bf r}) \cos({\bf q} \cdot {\bf R}) \\ m_z({\bf r}) \end{array} \right) }[/math]
This is schematically depicted in the figure at the top of this page: the components of the magnization in the xy-plane rotate about the spin-spiral propagation vector q.