Spin spirals: Difference between revisions
Vaspmaster (talk | contribs) No edit summary |
Vaspmaster (talk | contribs) |
||
| Line 2: | Line 2: | ||
== Generalized Bloch condition == | == Generalized Bloch condition == | ||
Spin spirals may be conveniently modeled using a | Spin spirals may be conveniently modeled using a generalization of the Bloch condition: | ||
<span id="GeneralizedBlochTheorem"> | <span id="GeneralizedBlochTheorem"> | ||
| Line 20: | Line 20: | ||
The latter is commonly chosen to lie within the first Brillouin zone of the reciprocal space lattice. | The latter is commonly chosen to lie within the first Brillouin zone of the reciprocal space lattice. | ||
This condition gives rise to the following | This generalized Bloch condition gives rise to the following behavior of the magnetization density: | ||
:<math> | :<math> | ||
Revision as of 12:47, 6 July 2018
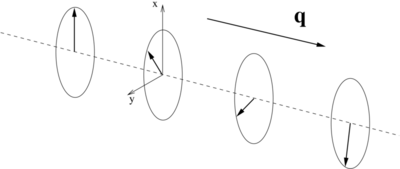
Generalized Bloch condition
Spin spirals may be conveniently modeled using a generalization of the Bloch condition:
i.e., from one unit cell to the next the up- and down-spinors pick up an additional phase factor of and , respectively. Here, R is a lattice vector of the crystalline lattice, and q is the so-called spin-spiral propagation vector. The latter is commonly chosen to lie within the first Brillouin zone of the reciprocal space lattice.
This generalized Bloch condition gives rise to the following behavior of the magnetization density:
This is schematically depicted in the figure at the top of this page: the components of the magnization in the xy-plane rotate about the spin-spiral propagation vector q.