Spin spirals: Difference between revisions
Vaspmaster (talk | contribs) |
Vaspmaster (talk | contribs) |
||
| Line 37: | Line 37: | ||
== Basis set considerations == | == Basis set considerations == | ||
The generalized Bloch condition redefines the Bloch functions as follows | The generalized Bloch condition redefines the Bloch functions as follows: | ||
:<math> | :<math> | ||
| Line 50: | Line 50: | ||
</math> | </math> | ||
This changes the Hamiltonian only minimally | This changes the Hamiltonian only minimally: | ||
:<math> | :<math> | ||
| Line 59: | Line 59: | ||
\left( \begin{array}{cc} | \left( \begin{array}{cc} | ||
H^{\uparrow\uparrow} & V^{\uparrow\downarrow}_{\rm xc} e^{-i\bf q \cdot \bf r} \\ | H^{\uparrow\uparrow} & V^{\uparrow\downarrow}_{\rm xc} e^{-i\bf q \cdot \bf r} \\ | ||
V^{\downarrow\uparrow}_{\rm xc}e^{+i\bf q \cdot \bf r} & H^{\downarrow\downarrow} \end{array}\right) | V^{\downarrow\uparrow}_{\rm xc}e^{+i\bf q \cdot \bf r} & H^{\downarrow\downarrow} \end{array}\right), | ||
</math> | </math> | ||
Revision as of 13:16, 6 July 2018
Generalized Bloch condition
Spin spirals may be conveniently modeled using a generalization of the Bloch condition (set LNONCOLLINEAR=.TRUE. and LSPIRAL=.TRUE.):
- [math]\displaystyle{ \left[ \begin{array}{c} \Psi^{\uparrow}_{\bf k}(\bf r) \\ \Psi^{\downarrow}_{\bf k}(\bf r) \end{array} \right] = \left( \begin{array}{cc} e^{-i\bf q \cdot \bf R / 2} & 0\\ 0 & e^{+i\bf q \cdot \bf R / 2} \end{array}\right) \left[ \begin{array}{c} \Psi^{\uparrow}_{\bf k}(\bf r-R) \\ \Psi^{\downarrow}_{\bf k}(\bf r-R) \end{array} \right], }[/math]
i.e., from one unit cell to the next the up- and down-spinors pick up an additional phase factor of [math]\displaystyle{ \exp(-i{\bf q}\cdot {\bf R}/2) }[/math] and [math]\displaystyle{ \exp(+i{\bf q}\cdot {\bf R}/2) }[/math], respectively, where R is a lattice vector of the crystalline lattice, and q is the so-called spin-spiral propagation vector.
The spin-spiral propagation vector is commonly chosen to lie within the first Brillouin zone of the reciprocal space lattice, and has to be specified by means of the QSPIRAL-tag.
The generalized Bloch condition above gives rise to the following behavior of the magnetization density:
- [math]\displaystyle{ {\bf m} ({\bf r} + {\bf R})= \left( \begin{array}{c} m_x({\bf r}) \cos({\bf q} \cdot {\bf R}) - m_y({\bf r}) \sin({\bf q} \cdot {\bf R}) \\ m_x({\bf r}) \sin({\bf q} \cdot {\bf R}) + m_y({\bf r}) \cos({\bf q} \cdot {\bf R}) \\ m_z({\bf r}) \end{array} \right) }[/math]
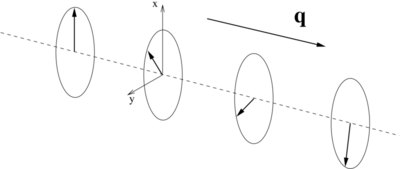
This is schematically depicted in the figure at the top of this page: the components of the magnization in the xy-plane rotate about the spin-spiral propagation vector q.
Basis set considerations
The generalized Bloch condition redefines the Bloch functions as follows:
- [math]\displaystyle{ \Psi^{\uparrow}_{\bf k}(\bf r) = \sum _{\bf G} \rm C^{\uparrow}_{\bf k \bf G} e^{i(\bf k + \bf G -\frac{\bf q}{2})\cdot \bf r} }[/math]
- [math]\displaystyle{ \Psi^{\downarrow}_{\bf k}(\bf r) = \sum _{\bf G} \rm C^{\downarrow}_{\bf k \bf G} e^{i(\bf k + \bf G +\frac{\bf q}{2})\cdot \bf r} }[/math]
This changes the Hamiltonian only minimally:
- [math]\displaystyle{ \left( \begin{array}{cc} H^{\uparrow\uparrow} & V^{\uparrow\downarrow}_{\rm xc} \\ V^{\downarrow\uparrow}_{\rm xc} & H^{\downarrow\downarrow} \end{array}\right) \rightarrow \left( \begin{array}{cc} H^{\uparrow\uparrow} & V^{\uparrow\downarrow}_{\rm xc} e^{-i\bf q \cdot \bf r} \\ V^{\downarrow\uparrow}_{\rm xc}e^{+i\bf q \cdot \bf r} & H^{\downarrow\downarrow} \end{array}\right), }[/math]
where in [math]\displaystyle{ H^{\uparrow\uparrow} }[/math] and [math]\displaystyle{ H^{\downarrow\downarrow} }[/math] the kinetic energy of a plane wave component changes to:
- [math]\displaystyle{ H^{\uparrow\uparrow}:\qquad |{\bf k} + {\bf G}|^2 \rightarrow |{\bf k} + {\bf G} - {\bf q} /2|^2 }[/math]
- [math]\displaystyle{ H^{\downarrow\downarrow}:\qquad |{\bf k} + {\bf G}|^2 \rightarrow |{\bf k} + {\bf G} + {\bf q} /2|^2 }[/math]