Spin spirals: Difference between revisions
Vaspmaster (talk | contribs) |
Vaspmaster (talk | contribs) |
||
| Line 87: | Line 87: | ||
G_{\rm ini}=\sqrt{\frac{2m}{\hbar^2}\mathtt{ENINI}} | G_{\rm ini}=\sqrt{\frac{2m}{\hbar^2}\mathtt{ENINI}} | ||
</math> | </math> | ||
In most cases it is more than sufficient to set {{TAG|ENMAX}}={{TAG|ENMAX}}<tt>+100</tt>. | |||
Revision as of 13:51, 6 July 2018
Generalized Bloch condition
Spin spirals may be conveniently modeled using a generalization of the Bloch condition (set LNONCOLLINEAR=.TRUE. and LSPIRAL=.TRUE.):
- [math]\displaystyle{ \left[ \begin{array}{c} \Psi^{\uparrow}_{\bf k}(\bf r) \\ \Psi^{\downarrow}_{\bf k}(\bf r) \end{array} \right] = \left( \begin{array}{cc} e^{-i\bf q \cdot \bf R / 2} & 0\\ 0 & e^{+i\bf q \cdot \bf R / 2} \end{array}\right) \left[ \begin{array}{c} \Psi^{\uparrow}_{\bf k}(\bf r-R) \\ \Psi^{\downarrow}_{\bf k}(\bf r-R) \end{array} \right], }[/math]
i.e., from one unit cell to the next the up- and down-spinors pick up an additional phase factor of [math]\displaystyle{ \exp(-i{\bf q}\cdot {\bf R}/2) }[/math] and [math]\displaystyle{ \exp(+i{\bf q}\cdot {\bf R}/2) }[/math], respectively, where R is a lattice vector of the crystalline lattice, and q is the so-called spin-spiral propagation vector.
The spin-spiral propagation vector is commonly chosen to lie within the first Brillouin zone of the reciprocal space lattice, and has to be specified by means of the QSPIRAL-tag.
The generalized Bloch condition above gives rise to the following behavior of the magnetization density:
- [math]\displaystyle{ {\bf m} ({\bf r} + {\bf R})= \left( \begin{array}{c} m_x({\bf r}) \cos({\bf q} \cdot {\bf R}) - m_y({\bf r}) \sin({\bf q} \cdot {\bf R}) \\ m_x({\bf r}) \sin({\bf q} \cdot {\bf R}) + m_y({\bf r}) \cos({\bf q} \cdot {\bf R}) \\ m_z({\bf r}) \end{array} \right) }[/math]
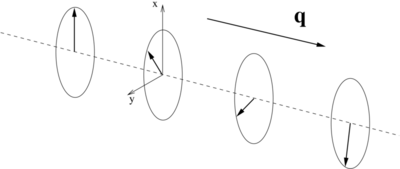
This is schematically depicted in the figure at the top of this page: the components of the magnization in the xy-plane rotate about the spin-spiral propagation vector q.
Basis set considerations
The generalized Bloch condition redefines the Bloch functions as follows:
- [math]\displaystyle{ \Psi^{\uparrow}_{\bf k}(\bf r) = \sum _{\bf G} \rm C^{\uparrow}_{\bf k \bf G} e^{i(\bf k + \bf G -\frac{\bf q}{2})\cdot \bf r} }[/math]
- [math]\displaystyle{ \Psi^{\downarrow}_{\bf k}(\bf r) = \sum _{\bf G} \rm C^{\downarrow}_{\bf k \bf G} e^{i(\bf k + \bf G +\frac{\bf q}{2})\cdot \bf r} }[/math]
This changes the Hamiltonian only minimally:
- [math]\displaystyle{ \left( \begin{array}{cc} H^{\uparrow\uparrow} & V^{\uparrow\downarrow}_{\rm xc} \\ V^{\downarrow\uparrow}_{\rm xc} & H^{\downarrow\downarrow} \end{array}\right) \rightarrow \left( \begin{array}{cc} H^{\uparrow\uparrow} & V^{\uparrow\downarrow}_{\rm xc} e^{-i\bf q \cdot \bf r} \\ V^{\downarrow\uparrow}_{\rm xc}e^{+i\bf q \cdot \bf r} & H^{\downarrow\downarrow} \end{array}\right), }[/math]
where in [math]\displaystyle{ H^{\uparrow\uparrow} }[/math] and [math]\displaystyle{ H^{\downarrow\downarrow} }[/math] the kinetic energy of a plane wave component changes to:
- [math]\displaystyle{ H^{\uparrow\uparrow}:\qquad |{\bf k} + {\bf G}|^2 \rightarrow |{\bf k} + {\bf G} - {\bf q} /2|^2 }[/math]
- [math]\displaystyle{ H^{\downarrow\downarrow}:\qquad |{\bf k} + {\bf G}|^2 \rightarrow |{\bf k} + {\bf G} + {\bf q} /2|^2 }[/math]
In the case of spin-spiral calculations the cutoff energy of the basis set of the individual spinor components is specified by means of the ENINI-tag.
Additionally one needs to set ENMAX appropriately: ENMAX needs to be chosen larger than ENINI, and large enough so that the plane wave components of both the up-spinors as well as the components of the down-spinor all have a kinetic energy smaller than ENMAX. This is the case when:
- [math]\displaystyle{ \mathtt{ENMAX}=\frac{\hbar^2}{2m}\left( G_{\rm ini} + |q| \right)^2 }[/math]
where
- [math]\displaystyle{ G_{\rm ini}=\sqrt{\frac{2m}{\hbar^2}\mathtt{ENINI}} }[/math]
In most cases it is more than sufficient to set ENMAX=ENMAX+100.