Equilibrium volume of Si in the RPA: Difference between revisions

Revision as of 17:09, 24 June 2019

Overview > bandgap of Si in GW > bandstructure of Si in GW (VASP2WANNIER90) > bandstructure of SrVO3 in GW > CRPA of SrVO3 > Equilibrium volume of Si in the RPA > List of tutorials

Task

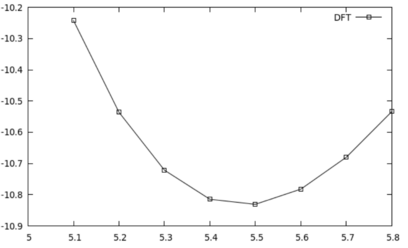
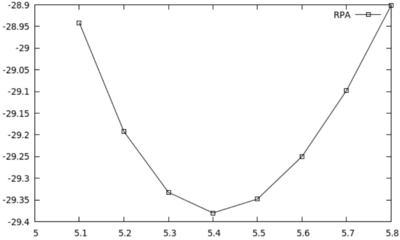
In this example you will calculate the equilibrium lattice constant of Si in the RPA (ACFDT).

The workflow of a RPA total energy calculations consists of five consecutive steps:

Step 1: a “standard” DFT groundstate calculation with a “dense” mesh of k-points.
Step 2: compute the Hartree-Fock energy using the DFT orbitals of Step 1. Needs WAVECAR file from step 1.
Step 3: a “standard” DFT groundstate calculation with “coarse” mesh of k-points.
Step 4: obtain DFT “virtual” orbitals (empty states). Needs WAVECAR file from step 3.
Step 5: the RPA correlation energy (ACFDT) calculation. Needs WAVECAR and WAVEDER files from step 4.

In case of metallic systems there is an additional step between Steps 4 and 5, that is beyond the scope of this example.

N.B.:To compute the equilibrium lattice constant of Si we need to calculate the RPA total energy for a range of different lattice constants. All of the calculation steps are prepared automatically performed by the script doall.sh (see below):

 ./doall.sh

This script will perform the following calculations for a range of different lattice constants:

Step 1: DFT groundstate calculation with a “dense” mesh of k-points

The following INCAR file is used (INCAR.DFT):

ISMEAR = 0 ; SIGMA = 0.05
EDIFF = 1E-8

The following KPOINTS file is used (KPOINTS.12):

Step 2: Compute the Hartree-Fock energy using the DFT orbitals

To Compute the Hartree-Fock energy using DFT orbitals we need the (WAVECAR) of Step 1.

The INCAR file INCAR.EXX is used in this step:

 {{TAGBL|ALGO}} = EIGENVAL ; {{TAGBL|NELM}} = 1
 {{TAGBL|LWAVE}} = .FALSE.
 {{TAGBL|LHFCALC}} = .TRUE.
 {{TAGBL|AEXX}} = 1.0 ; {{TAGBL|ALDAC}} = 0.0 ; {{TAGBL|AGGAC}} = 0.0
 {{TAGBL|NKRED}} = 2
 {{TAGBL|ISMEAR}} = 0 ; {{TAGBL|SIGMA}} = 0.05
 {{TAGBL|KPAR}} = 8
 {{TAGBL|NBANDS}} = 4

NKRED=2 is used for the downsample the k-space representation of the Fock-potential to save time.

Using NBANDS=4 only occupied states are considered to save time.

Step 3: DFT groundstate calculation with a “coarse” mesh of k-points

Perform a DFT groundstate calculation with a “coarse” mesh of k-points.

The following INCAR file is used (INCAR.DFT):

ISMEAR = 0 ; SIGMA = 0.05
EDIFF = 1E-8

The following coarse KPOINTS file is used (KPOINTS.6):

Step 4: Obtain DFT "virtual" orbitals (empty states)

Obtain DFT "virtual" orbitals (empty states).

The following INCAR file is used in this step (INCAR.DIAG):

ALGO = Exact
NBANDS = 64
NELM = 1
LOPTICS = .TRUE.
ISMEAR = 0 ; SIGMA = 0.05

In this step one needs to set LOPTICS=.TRUE. so that VASP calculates the derivative of the orbitals w.r.t. the Bloch wavevector (stored in the WAVEDER file). These are needed to correctly describe the long-wavelength limit of the dielectric screening.
We use exact diagonalization (ALGO=Exact) and keep 64 bands after diagonalization (NBANDS=64).
This calculations needs the orbitals (WAVECAR file) written in Step 3.

Step 5: calculate the RPA correlation energy (ACFDT)

The following INCAR file is used in this step (INCAR.ACFDT):

ALGO = ACFDT
NBANDS = 64
ISMEAR = 0 ; SIGMA = 0.05

In OUTCAR.ACFDT.X.X one finds the RPA correlation energy, e.g.:

        cutoff energy      smooth cutoff    RPA   correlation   Hartree contr. to MP2
 ---------------------------------------------------------------------------------
             163.563            130.851       -10.7869840331      -19.0268026572
             155.775            124.620       -10.7813600055      -19.0200457142
             148.357            118.685       -10.7744584182      -19.0118291822
             141.292            113.034       -10.7659931963      -19.0017871991
             134.564            107.651       -10.7555712745      -18.9894197881
             128.156            102.525       -10.7428704760      -18.9742991317
             122.054             97.643       -10.7273118140      -18.9556871679
             116.241             92.993       -10.7085991597      -18.9331679971
 linear regression
 converged value                              -10.9079580568      -19.1711146204

Take the “converged value”, in this case: EC(RPA) = -10.9079580568eV (an approximate “infinite basis set” limit).

This calculations needs the orbitals (WAVECAR file) and the derivative of the orbitals w.r.t. the Bloch wavevectors (WAVEDER file) written in Step 4.

The RPA total energy is calculated as the, E(RPA)=EC(RPA)+EXX, the sum of the RPA correlation energy of step 5 EC(RPA) and the Hartree fock energy EXX of step 2.

To get the Hartree fock energy grep “free energy” in the OUTCAR.EXX.* file (there are two spaces between free and energy).

Running this example

The following bash-script doall.sh will run through all of the aforementioned calculational steps (step 1-5) for a range of different lattice constants (a=5.1-5.8Å in steps of 0.1Å)

#
# To run VASP this script calls $vasp_std
# (or posibly $vasp_gam and/or $vasp_ncl).
# These variables can be defined by sourcing vaspcmd
. vaspcmd 2> /dev/null

#
# When vaspcmd is not available and $vasp_std,
# $vasp_gam, and/or $vasp_ncl are not set as environment
# variables, you can specify them here
[ -z "`echo $vasp_std`" ] && vasp_std="mpirun -np 8 /path-to-your-vasp/vasp_std"
[ -z "`echo $vasp_gam`" ] && vasp_gam="mpirun -np 8 /path-to-your-vasp/vasp_gam"
[ -z "`echo $vasp_ncl`" ] && vasp_ncl="mpirun -np 8 /path-to-your-vasp/vasp_ncl"

#
# The real work starts here
#

for i in  5.1 5.2 5.3 5.4 5.5 5.6 5.7 5.8 ; do

cat >POSCAR <<!
system Si
  $i
0.5 0.5 0.0
0.0 0.5 0.5
0.5 0.0 0.5
2
cart
0.00 0.00 0.00
0.25 0.25 0.25
!

# start with a PBE calculation with a lot of k-points (needed for EXX)
rm WAVECAR WAVEDER
cp KPOINTS.12 KPOINTS
cp INCAR.DFT INCAR
$vasp_std

cp OUTCAR OUTCAR.DFT.$i
e1=`awk '/free  energy/ {print $5}' OUTCAR`

# get the HF energy with PBE orbitals
cp INCAR.EXX INCAR
$vasp_std
e2=`awk '/free  energy/ {print $5}' OUTCAR`

cp OUTCAR OUTCAR.EXX.$i

# now a PBE calculation with less k-points
rm WAVECAR WAVEDER
cp KPOINTS.6 KPOINTS
cp INCAR.DFT INCAR
$vasp_std

# obtain virtual orbitals
cp INCAR.DIAG INCAR
$vasp_std

cp OUTCAR OUTCAR.DIAG.$i
cp WAVECAR WAVECAR.$i
cp WAVEDER WAVEDER.$i

## for metals
# cp INCAR.HFC INCAR
# $vasp_std
#
# cp OUTCAR OUTCAR.HFC.$i
# e3=`awk '/HF-correction/ {print $4}' OUTCAR`

# RPA correlation
cp INCAR.ACFDT INCAR
$vasp_std

cp OUTCAR OUTCAR.ACFDT.$i
e4=`awk '/converged value/ {print $3}' OUTCAR`

# echo $i $e1 $e2 $e3 $e4 >> summary
echo $i $e1 $e2 $e4 >> summary

done

To execute the aforementions script: