Liquid Si - MLFF
Task
Generating a machine learning force field for liquid Si. For this tutorial, we expect that the user is already familiar with running conventional ab initio molecular dynamic calculations.
Input
POSCAR
In this example we start from a 64 atom super cell of diamond-fcc Si (the same as in Liquid Si - Standard MD):
Si cubic diamond 2x2x2 super cell of conventional cell
5.43090000000000
2.00000000 0.00000000 0.00000000
0.00000000 2.00000000 0.00000000
0.00000000 0.00000000 2.00000000
Si
64
Direct
0.00000000 0.00000000 0.00000000
0.50000000 0.00000000 0.00000000
0.00000000 0.50000000 0.00000000
0.50000000 0.50000000 0.00000000
0.00000000 0.00000000 0.50000000
0.50000000 0.00000000 0.50000000
0.00000000 0.50000000 0.50000000
0.50000000 0.50000000 0.50000000
0.37500000 0.12500000 0.37500000
0.87500000 0.12500000 0.37500000
0.37500000 0.62500000 0.37500000
0.87500000 0.62500000 0.37500000
0.37500000 0.12500000 0.87500000
0.87500000 0.12500000 0.87500000
0.37500000 0.62500000 0.87500000
0.87500000 0.62500000 0.87500000
0.00000000 0.25000000 0.25000000
0.50000000 0.25000000 0.25000000
0.00000000 0.75000000 0.25000000
0.50000000 0.75000000 0.25000000
0.00000000 0.25000000 0.75000000
0.50000000 0.25000000 0.75000000
0.00000000 0.75000000 0.75000000
0.50000000 0.75000000 0.75000000
0.37500000 0.37500000 0.12500000
0.87500000 0.37500000 0.12500000
0.37500000 0.87500000 0.12500000
0.87500000 0.87500000 0.12500000
0.37500000 0.37500000 0.62500000
0.87500000 0.37500000 0.62500000
0.37500000 0.87500000 0.62500000
0.87500000 0.87500000 0.62500000
0.25000000 0.00000000 0.25000000
0.75000000 0.00000000 0.25000000
0.25000000 0.50000000 0.25000000
0.75000000 0.50000000 0.25000000
0.25000000 0.00000000 0.75000000
0.75000000 0.00000000 0.75000000
0.25000000 0.50000000 0.75000000
0.75000000 0.50000000 0.75000000
0.12500000 0.12500000 0.12500000
0.62500000 0.12500000 0.12500000
0.12500000 0.62500000 0.12500000
0.62500000 0.62500000 0.12500000
0.12500000 0.12500000 0.62500000
0.62500000 0.12500000 0.62500000
0.12500000 0.62500000 0.62500000
0.62500000 0.62500000 0.62500000
0.25000000 0.25000000 0.00000000
0.75000000 0.25000000 0.00000000
0.25000000 0.75000000 0.00000000
0.75000000 0.75000000 0.00000000
0.25000000 0.25000000 0.50000000
0.75000000 0.25000000 0.50000000
0.25000000 0.75000000 0.50000000
0.75000000 0.75000000 0.50000000
0.12500000 0.37500000 0.37500000
0.62500000 0.37500000 0.37500000
0.12500000 0.87500000 0.37500000
0.62500000 0.87500000 0.37500000
0.12500000 0.37500000 0.87500000
0.62500000 0.37500000 0.87500000
0.12500000 0.87500000 0.87500000
0.62500000 0.87500000 0.87500000
KPOINTS
We will start with a single k point in this example:
K-Points 0 Gamma 1 1 1 0 0 0
INCAR
#Basic parameters ISMEAR = 0 SIGMA = 0.1 LREAL = Auto ALGO = FAST ISYM = -1 NELM = 100 EDIFF = 1E-4 LWAVE = .FALSE. LCHARG = .FALSE. #Parallelization of ab initio calculations NCORE = 2 #MD IBRION = 0 MDALGO = 2 ISIF = 2 SMASS = 1.0 TEBEG = 2000 NSW = 10000 POTIM = 3.0 #Parameters for initialization of wavefunctions and charge density INIWAV = 1 IWAVPR = 1 ISTART = 0 ICHARG = 0 #Machine learning paramters ML_FF_LMLFF = .TRUE. ML_FF_ISTART = 0 ML_FF_NWRITE = 2 ML_FF_EATOM = -.70128086E+00
- ML_FF_LMLFF = .TRUE.
- switches on the machine learning of the force field
- ML_FF_ISTART = 0
- corresponds to learning from scratch
- ML_FF_NWRITE = 2
- leads to a more verbose output where the error on energies, forces and stress are written to the ML_LOGFILE file. This setting is very handy to check the accuracy of the force field.
- ML_FF_EATOM = -.70128086E+00
- sets the atomic reference energy for each species. We show to obtain this energy below.
- IWAVPR = 1
- extrapolates the total charge density from the atomic ones. This is more advisable than the default, because during the on-the-fly learning several hundreds or thousands of molecular dynamics steps can lie between two ab initio calculations.
Calculation
Reference energy
To obtain the force field for liquid Si, we require the atomic energy of a single Si atom. We create a new working directory for this calculation
mkdir Si_ATOM cd Si_ATOM ln -s ../POTCAR
In this directory, we create the following INCAR file
#Basic parameters ISMEAR = 0 SIGMA = 0.1 LREAL = Auto ALGO = FAST ISYM = 0 NELM = 100 EDIFF = 1E-4 LWAVE = .FALSE. LCHARG = .FALSE. ISPIN = 2
The POSCAR file contains a single atom in a large enough box (the box should be orthorhombic to have enough degrees of freedom for electronic relaxation)
Si atom
1.00090000000000
12.00000000 0.00000000 0.00000000
0.00000000 12.01000000 0.00000000
0.00000000 0.00000000 12.02000000
Si
1
Direct
0.00000000 0.00000000 0.00000000
Due to the large unit cell, we can use a Gamma point calculation set up in the KPOINTS file
Gamma point only 0 0 0 Gamma 1 1 1 0 0 0
After running the calculation, we obtain the total energy from the OUTCAR or OSZICAR file. We use this energy for the ML_FF_EATOM tag. If multiple atom types are present in the structure, this step has to be repeated for each atom type separately and the reference energies are provided as a list after the ML_FF_EATOM tag. The ordering of the energies corresponds to the ordering of the elements in the POTCAR file.
Creating the liquid structure
Because we don't have a structure of liquid silicon readily available, we first create that structure by starting from a super cell of crystalline silicon with 64 atoms. The temperature is set to 2000 K so that the crystal melts rapidly in the MD run. To improve the simulation speed drastically, we utilize the on-the-fly machine learning. Most of the ab initio steps will be replaced by very fast force-field ones. Within 10000 steps equivalent to 30 ps, we have obtained a good starting position for the subsequent simulations in the CONTCAR file. You can copy the input files or download them.
After running the calculation, we obtained a force field, but its initial trajectory might be tainted but the unreasonable starting position. Nevertheless, it is instructive to inspect the output to understand how to assess the accuracy of a force field, before refining it in subsequent calculations. The main output files for the machine learning are
- ML_ABNCAR
- contains the ab initio structure datasets used for the learning. It will be needed for continuation runs as ML_ABCAR.
- ML_FFNCAR
- contains the regression results (weights, parameters, etc.). It will be needed for continuation runs as ML_FFCAR.
- ML_LOGFILE
- logging the proceedings of the machine learning. With ML_FF_NWRITE = 2 set, this file lists the error between force-field and ab initio calculation for energy, forces and the stress. The entry for the last step should be similar to the following (the inherent randomness of a molecular dynamics simulation will lead to slightly different results):
====================================================================================================
Information on error estimations
----------------------------------------------------------------------------------------------------
Error in energy (eV atom^-1): 0.016994
Error in force (eV Angst^-1): 0.247664
Error in stress (kB): 5.368218
Bayesian error (eV Angst-1): 0.064904 0.127195
Spilling factor (-): 0.000690 0.020000
====================================================================================================
You can see that additional information about the Bayesian error and the spilling factor is reported. The first entry of the Bayesian error is the estimated error from our model. If the estimated error exceeds the threshold listed next to it a new structure dataset is generated. The threshold is automatically determined during the calculations. The first and second entry for the spilling factor are the calculated spilling factor and the threshold, respectively. The threshold for the spilling factor is usually always kept constant during the calculations.
Structral properties of the force field
Next we will look at the accuracy of structural properties of the force field. For the we first run a 3000 fs molecular dynamics calculation with and without the force field starting from the new CONTCAR file. First we save that new CONTCAR file to
cp CONTCAR POSCAR.T2000_relaxed
Now do the following steps to run the force field calculation:
- Copy POSCAR.T2000_relaxed to POSCAR.
- Copy ML_ABNCAR to ML_ABCAR.
- Copy ML_FFNCAR to ML_FFCAR.
- Change INCAR tags:
- Change ML_FF_ISTART=0 to ML_FF_ISTART=2: This will switch of learning and only use the machine-learned force field.
- Change NSW=10000 to NSW=1000.
- Run calculation.
- Copy XDATCAR to XDATCAR.MLFF_3ps.
Now do the following steps to run the ab initio reference calculation:
- Copy POSCAR.T2000_relaxed to POSCAR.
- Change ML_FF_LMLFF=.TRUE. to {TAG|ML_FF_LMLFF}}=.FALSE.: This will turn off the machine learning completely.
- Run caclulation.
- Copy XDATCAR to XDATCAR.AI_3ps.
To analyze the pair correlation function use the PERL script pair_correlation_function.pl:
#!/usr/bin/perl
use strict;
use warnings;
#configuration for which ensemble average is to be calculated
my $confmin=1; #starting index of configurations in XDATCAR file for pair correlation function
my $confmax=20000; #last index of configurations in XDATCAR file for pair correlation function
my $confskip=1; #stepsize for configuration loop
my $species_1 = 1; #species 1 for which pair correlation function is going to be calculated
my $species_2 = 1; #species 2 for which pair correlation function is going to be calculated
#setting radial grid
my $rmin=0.0; #minimal value of radial grid
my $rmax=10.0; #maximum value of radial grid
my $nr=300; #number of equidistant steps in radial grid
my $dr=($rmax-$rmin)/$nr; #stepsize in radial grid
my $tol=0.0000000001; #tolerance limit for r->0
my $z=0; #counter
my $numelem; #number of elements
my @elements; #number of atoms per element saved in list/array
my $lattscale; #scaling factor for lattice
my @b; #Bravais matrix
my $nconf=0; #number of configurations in XDATCAR file
my @cart; #Cartesian coordinates for each atom and configuration
my $atmin_1=0; #first index of species one
my $atmax_1; #last index of species one
my $atmin_2=0; #first index of species two
my $atmax_2; #last index of species two
my @vol; #volume of cell (determinant of Bravais matrix)
my $pi=4*atan2(1, 1); #constant pi
my $natom=0; #total number of atoms in cell
my @pcf; #pair correlation function (list/array)
my $mult_x=1; #periodic repetition of cells in x dimension
my $mult_y=1; #periodic repetition of cells in y dimension
my $mult_z=1; #periodic repetition of cells in z dimension
my @cart_super; #Cartesian cells over multiple cells
my @vec_len; #Length of lattice vectors in 3 spatial coordinates
#my $ensemble_type="NpT"; #Set Npt or NVT. Needs to be set since both have different XDATCAR file.
my $ensemble_type="NVT"; #Set Npt or NVT. Needs to be set since both have different XDATCAR file.
my $av_vol=0; #Average volume in cell
#reading in XDATCAR file
while (<>)
{
chomp;
$_=~s/^/ /;
my @help=split(/[\t,\s]+/);
$z++;
if ($z==2)
{
$lattscale = $help[1];
}
if ($z==3)
{
$b[$nconf+1][1][1]=$help[1]*$lattscale;
$b[$nconf+1][1][2]=$help[2]*$lattscale;
$b[$nconf+1][1][3]=$help[3]*$lattscale;
}
if ($z==4)
{
$b[$nconf+1][2][1]=$help[1]*$lattscale;
$b[$nconf+1][2][2]=$help[2]*$lattscale;
$b[$nconf+1][2][3]=$help[3]*$lattscale;
}
if ($z==5)
{
$b[$nconf+1][3][1]=$help[1]*$lattscale;
$b[$nconf+1][3][2]=$help[2]*$lattscale;
$b[$nconf+1][3][3]=$help[3]*$lattscale;
}
if ($z==7)
{
if ($nconf==0)
{
$numelem=@help-1;
for (my $i=1;$i<=$numelem;$i++)
{
$elements[$i]=$help[$i];
$natom=$natom+$help[$i];
}
}
}
if ($_=~m/Direct/)
{
$nconf=$nconf+1;
#for NVT ensemble only one Bravais matrix exists, so it has to be copied
if ($ensemble_type eq "NVT")
{
for (my $i=1;$i<=3;$i++)
{
for (my $j=1;$j<=3;$j++)
{
$b[$nconf][$i][$j]=$b[1][$i][$j];
}
}
}
for (my $i=1;$i<=$natom;$i++)
{
$_=<>;
chomp;
$_=~s/^/ /;
my @helpat=split(/[\t,\s]+/);
$cart[$nconf][$i][1]=$b[1][1][1]*$helpat[1]+$b[1][1][2]*$helpat[2]+$b[1][1][3]*$helpat[3];
$cart[$nconf][$i][2]=$b[1][2][1]*$helpat[1]+$b[1][2][2]*$helpat[2]+$b[1][2][3]*$helpat[3];
$cart[$nconf][$i][3]=$b[1][3][1]*$helpat[1]+$b[1][3][2]*$helpat[2]+$b[1][3][3]*$helpat[3];
}
if ($ensemble_type eq "NpT")
{
$z=0;
}
}
last if eof;
}
if ($confmin>$nconf)
{
print "Error, confmin larger than number of configurations. Exiting...\n";
exit;
}
if ($confmax>$nconf)
{
$confmax=$nconf;
}
for (my $i=1;$i<=$nconf;$i++)
{
#calculate lattice vector lengths
$vec_len[$i][1]=($b[$i][1][1]*$b[$i][1][1]+$b[$i][1][2]*$b[$i][1][2]+$b[$i][1][3]*$b[$i][1][3])**0.5;
$vec_len[$i][2]=($b[$i][2][1]*$b[$i][2][1]+$b[$i][2][2]*$b[$i][2][2]+$b[$i][2][3]*$b[$i][2][3])**0.5;
$vec_len[$i][3]=($b[$i][3][1]*$b[$i][3][1]+$b[$i][3][2]*$b[$i][3][2]+$b[$i][3][3]*$b[$i][3][3])**0.5;
#calculate volume of cell
$vol[$i]=$b[$i][1][1]*$b[$i][2][2]*$b[$i][3][3]+$b[$i][1][2]*$b[$i][2][3]*$b[$i][3][1]+$b[$i][1][3]*$b[$i][2][1]*$b[$i][3][2]-$b[$i][3][1]*$b[$i][2][2]*$b[$i][1][3]-$b[$i][3][2]*$b[$i][2][3]*$b[$i][1][1]-$b[$i][3][3]*$b[$i][2][1]*$b[$i][1][2];
$av_vol=$av_vol+$vol[$i];
}
$av_vol=$av_vol/$nconf;
#choose species 1 for which pair correlation function is going to be calculated
$atmin_1=1;
if ($species_1>1)
{
for (my $i=1;$i<$species_1;$i++)
{
$atmin_1=$atmin_1+$elements[$i];
}
}
$atmax_1=$atmin_1+$elements[$species_1]-1;
#choose species 2 to which paircorrelation function is calculated to
$atmin_2=1;
if ($species_2>1)
{
for (my $i=1;$i<$species_2;$i++)
{
$atmin_2=$atmin_2+$elements[$i];
}
}
$atmax_2=$atmin_2+$elements[$species_2]-1;
#initialize pair correlation function
for (my $i=0;$i<=($nr-1);$i++)
{
$pcf[$i]=0.0;
}
# loop over configurations, make histogram of pair correlation function
for (my $j=$confmin;$j<=$confmax;$j=$j+$confskip)
{
for (my $k=$atmin_1;$k<=$atmax_1;$k++)
{
for (my $l=$atmin_2;$l<=$atmax_2;$l++)
{
if ($k==$l) {next};
for (my $g_x=-$mult_x;$g_x<=$mult_x;$g_x++)
{
for (my $g_y=-$mult_y;$g_y<=$mult_y;$g_y++)
{
for (my $g_z=-$mult_y;$g_z<=$mult_z;$g_z++)
{
my $at2_x=$cart[$j][$l][1]+$vec_len[$j][1]*$g_x;
my $at2_y=$cart[$j][$l][2]+$vec_len[$j][2]*$g_y;
my $at2_z=$cart[$j][$l][3]+$vec_len[$j][3]*$g_z;
my $dist=($cart[$j][$k][1]-$at2_x)**2.0+($cart[$j][$k][2]-$at2_y)**2.0+($cart[$j][$k][3]-$at2_z)**2.0;
$dist=$dist**0.5;
#determine integer multiple
my $zz=int(($dist-$rmin)/$dr+0.5);
if ($zz<$nr)
{
$pcf[$zz]=$pcf[$zz]+1.0;
}
}
}
}
}
}
}
#make ensemble average, rescale functions and print
for (my $i=0;$i<=($nr-1);$i++)
{
my $r=$rmin+$i*$dr;
if ($r<$tol)
{
$pcf[$i]=0.0;
}
else
{
$pcf[$i]=$pcf[$i]*$av_vol/(4*$pi*$r*$r*$dr*(($confmax-$confmin)/$confskip)*($atmax_2-$atmin_2+1)*($atmax_1-$atmin_1+1));#*((2.0*$mult_x+1.0)*(2.0*$mult_y+1.0)*(2.0*$mult_z+1.0)));
}
print $r," ",$pcf[$i],"\n";
}
Obtain the pair correlation function from the previously saved XDATCAR files:
perl pair_correlation_function.pl XDATCAR.MLFF_3ps > pair_MLFF_3ps.dat perl pair_correlation_function.pl XDATCAR.AI_3ps > pair_AI_3ps.dat
Plot the pair correlation functions using the following command:
gnuplot -e "set terminal jpeg; set xlabel 'r(Ang)'; set ylabel 'PCF'; set style data lines; plot 'pair_MLFF_3ps.dat', 'pair_AI_3ps.dat' " > PC_MLFF_vs_AI_3ps.jpg
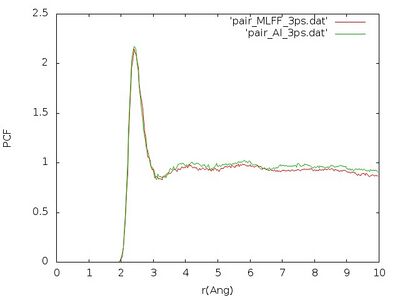
The pair correlation functions obtained that way should look similar like that:
We see that pair correlation is quite well reproduced although the error on the force is a little bit large. Nevertheless we just used this learning to very create a liquid structure very fast, since creating a liquid from a perfect crystal can be a time consuming task.
Obtaining more accurate force field
Including the melting phase in the force field may impact the accuracy of the force field. To improve it is usually advisable to learn on the pure structures, which in our case this means to use the CONTCAR file obtained after the melting. Furthermore, the force field was learned using only a single k point so that we can improve the accuracy of the reference data by including more k points. After learning how to get a good starting structure for the the liquid we will restart the learning but with better ab initio parameters using the CONTCAR from the previous subsection. It is important in most calculations to have quite accurate ab initio calculations since bad ab initio parameters can really limit the accuracy of the learning or even inhibit a proper learning.
We do the following steps to restart learning:
- Copy POSCAR.T2000_relaxed to POSCAR.
- Change INCAR tags:
- Set ALGO=Normal.
- Set ML_FF_LMLFF=.FALSE. back to ML_FF_LMLFF=.TRUE..
- Set ML_FF_ISTART=2 back to ML_FF_ISTART=0.
- Set NSW=1000 back to NSW=10000. We will learn again for 30 ps.
- Optionally add k point parallelization wth the KPAR tag (if you are not familiar with this tag leave it be).
- Increase the k mesh in the KPOINTS file. The new file looks like:
test 0 0 0 Gamma 2 2 2 0 0 0
- Run the calculation using the standard version of VASP (usually vasp_std).
After running the calculation we will again look at the error in the ML_LOGFILE, where the obtained values should be close to:
====================================================================================================
Information on error estimations
----------------------------------------------------------------------------------------------------
Error in energy (eV atom^-1): 0.006079
Error in force (eV Angst^-1): 0.165678
Error in stress (kB): 2.553148
Bayesian error (eV Angst-1): 0.044695 0.101357
Spilling factor (-): 0.002285 0.020000
====================================================================================================
We immediately see that the errors are significantly lower than in the training with one k point.
Next we try to look at how well the force field is learned and try to monitor how much training data is added to a structure after each learning cycle.
The ML_ABNCAR file contains the training data. The number of reference structures and the basis-set size are written at the beginning of this file. The values in this example at this step should be close to the following:
**************************************************
The number of configurations
--------------------------------------------------
55
and
**************************************************
The numbers of basis sets per atom type
--------------------------------------------------
396
for the training-set size and basis-set size, respectively.
Now we want to further continue the learning to see how much data is added and how the accuracy of the force field changes. Do the following steps for a continuation run with on-the-fly learning:
- Copy ML_ABNCAR to ML_ABCAR.
- Copy CONTCAR to POSCAR.
- Modify the INCAR file in the following way:
- Change ML_FF_ISTART=0 to ML_FF_ISTART=1.
- Add ML_FF_CTIFOR=x, where x is the last criterion for the threshold of the Bayesian error obtained from the ML_LOGFILE (from the entry above it would be 0.101357, but please use the value that you obtained in your calculation). By setting already a good guess for the threshold several ab initio steps can be skipped from the beginning which would be required to determine the Bayesian error criterion. Mind: When continuation runs are performed where the crystal structure is changed, the last obtained error criterion for the Bayesian error can be too large and then many ab initio steps can be skipped wrongly (this can especially happen when going from first a liquid to a solid phase). In that case it is safer to use the default of ML_FF_CTIFOR=10^{-16}</math>}}.
After learning we again look at the last entry of the errors in the ML_LOGFILE, which should look like:
====================================================================================================
Information on error estimations
----------------------------------------------------------------------------------------------------
Error in energy (eV atom^-1): 0.006252
Error in force (eV Angst^-1): 0.168549
Error in stress (kB): 2.606332
Bayesian error (eV Angst-1): 0.037569 0.101357
Spilling factor (-): 0.001114 0.020000
====================================================================================================
We see that the accuracy has not significantly changed. Also the threshold for the Bayesian error has not change (by typing grep "Bayesian error (eV Angst-1):" ML_LOGFILE we see that it was the same the whole time). By looking at the actual errors we see that that the threshold was overwritten only very few times. To see how often the threshold was overstepped type the following command on the command line:
grep "Bayesian error (eV Angst-1):" ML_LOGFILE |awk '{if ($5>0.101357) {print $5}}'
Consequently only very few structures were added to the ab initio data in the ML_ABNCAR file. The entry for the reference structures and basis sets should look like:
**************************************************
The number of configurations
--------------------------------------------------
65
and
**************************************************
The numbers of basis sets per atom type
--------------------------------------------------
407
This means that either the force field is already accurate enough or that the threshold is set too high and ab initio calculations are skipped because the force field is too accurate for that criterion.
Next we will test the learning with the default value for ML_FF_CTIFOR (which is practically zero), to see if the force field changes significantly. For that the following steps have to be done:
After rerunning the calculation we see that many structures have been added in the ML_ABNCAR file:
**************************************************
The number of configurations
--------------------------------------------------
160
...
**************************************************
The numbers of basis sets per atom type
--------------------------------------------------
726
Nevertheless the accuracy of the force field did not improve significantly in the ML_LOGFILE:
====================================================================================================
Information on error estimations
----------------------------------------------------------------------------------------------------
Error in energy (eV atom^-1): 0.005950
Error in force (eV Angst^-1): 0.162064
Error in stress (kB): 2.628567
Bayesian error (eV Angst-1): 0.029723 0.061348
Spilling factor (-): 0.000406 0.020000
====================================================================================================
Ideally one should continue learning until no structures need to be added to the training data and basis set any more. Practically this is hard to achieve, since the prediction of the Bayesian error has some inaccuracies and learning can be executed even if the force field is accurate enough. Nevertheless for practical calculations one has to stop the calculation at a given point. In this example we stop here because the accuracy on test structures compared to the ab initio data is not improving in the ML_LOGFILE by further addition of training data and this example is only a tutorial example. For high quality production calculations suited for publications we would advise to learn until almost no data is added to the training structures and basis set. In many cases this involves a length of 100 ps for learning.
User task: The user should continue learning and observe the convergence of the number of reference structures. Most likely the maximum allowed basis set size ML_FF_MB_MB needs to be increased. The user should also look at the pair correlation function with respect to the ab initio data. Is it still ok?
Optimizing weights on energy, forces and stress
Next we learn how to refine an existing force after it has been learned. We will use the force field already obtained from the previous subsection. In this wiki we show the results for the force field learned for 30 ps. If one has learned for a longer time (user task in the previous example) one can also use that force field, but should of course expect larger deviations from the results presented here. The input parameters ML_FF_WTOTEN, ML_FF_WTIFOR and ML_FF_WTSIF are the weights for energy, force and stress in the linear fitting, respectively. By default they are set to 1.0, so energy, force and stress are weighted equally. The weights are relative weights, this means it is sufficient to increase only the weight of interest, while keeping the other parameters at 1.0. If the weight for a component is increased the error of that component usually becomes lower with higher weight. Simultaneously the error on the other components gets worse, but at a different rate. For a given optimal value of the weight the overall error can be minimized, such that the component of interest is reproduced with much more accuracy. Usually this can be important for methods where the free energy is important (such as e.g. Interface pinning calculations, Metadynamics etc.) and this weighting can improve the error on energy significantly while only slightly making the errors on forces and stress worse.
To run the weight optimizations calculations the following steps are necessary:
- Copy INCAR to INCAR.run. This will serve as a template since several short calculations will be executed with different weights for the energy.
- Copy CONTCAR to POSCAR.run. For each calculation the same POSCAR file needs to be used as a starting point.
- Copy ML_ABNCAR to ML_ABCAR.
- Modify INCAR.run as follows:
- Set ML_FF_ISTART=1.
- Set NSW=1. We will only need a single new test structure.
- The ML_FF_WTOTEN test will be added by the runscript.
- Use the bash script run_param_opt.sh (or use your own) which contains the following lines:
#!/bin/bash
if [ -f error_vs_eweight.dat ]; then
rm error_vs_eweight.dat
fi
touch error_vs_eweight.dat
for i in 1.0 1.5 2.0 2.5 3.0 3.5 4.0 4.5 5.0
do
cat INCAR.run > INCAR
echo "ML_FF_WTOTEN = $i" >> INCAR
cp POSCAR.run POSCAR
mpirun -np $np $executable_path/vasp_std
cp ML_LOGFILE ML_LOGFILE.$i
awk -v var="$i" '/Error in energy \(eV atom\^-1\)\:/{energy=$6} /Error in force \(eV Angst\^-1\)\:/ {force=$6} /Error in stress \(kB\)\:/{stress=$5} /Energy SD. \(eV atom\^-1\)\:/{energy_var=$5} /Force SD. \(eV Angst\^-1\)\:/{force_var=$5} /Stress SD. \(kB\)\:/ {stress_var=$4} END{print var,energy/energy_var+force/force_var+stress/stress_var}' ML_LOGFILE.$i >> error_vs_eweight.dat
done
The user needs to set the executable path $executable_path in this directory (and maybe the executable name). This script adds the weight for the energy ML_FF_WTOTEN = $i to the INCAR file, where $i runs from 1.0 to 5.0 with a step size of 0.5. After that a single step calculation is performed. The errors compared to ab initio and standard deviations for energies, forces and stress are output to the ML_LOGFILE and from that file the sum of the normalized errors is plotted against the weight of the energy. The normalization is done by dividing the errors by the standard deviation for each component.
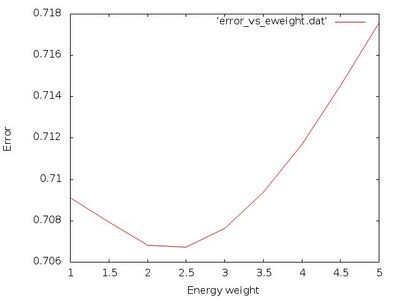
The normalized total error vs. weight for the energy is plotted from the file error_vs_eweight.dat:
gnuplot -e "set terminal jpeg; set xlabel 'Energy weight'; set ylabel 'Error'; set style data lines; plot 'error_vs_eweight.dat'" > error_vs_eweight.jpg
It should look similar to:
From this plot we see that an ideal value is around ML_FF_WTOTEN=2.5. Next we take a look at the actual errors for that weighting parameter in the file ML_LOGFILE.2.5:
====================================================================================================
Information on error estimations
----------------------------------------------------------------------------------------------------
Error in energy (eV atom^-1): 0.005322
Error in force (eV Angst^-1): 0.169356
Error in stress (kB): 2.849817
Bayesian error (eV Angst-1): 0.025548 0.000000
Spilling factor (-): 0.000368 0.020000
====================================================================================================
We see that the error on energy decreased while it increased for forces and stress compared to ML_LOGFILE.1.0:
====================================================================================================
Information on error estimations
----------------------------------------------------------------------------------------------------
Error in energy (eV atom^-1): 0.005954
Error in force (eV Angst^-1): 0.162006
Error in stress (kB): 2.628128
Bayesian error (eV Angst-1): 0.028542 0.000000
Spilling factor (-): 0.000368 0.020000
====================================================================================================
In this example the decrease of the energy is only small but in many examples this can lead to signifcant increase in the precision.
Here are the errors for ML_LOGFILE_5.0:
====================================================================================================
Information on error estimations
----------------------------------------------------------------------------------------------------
Error in energy (eV atom^-1): 0.004692
Error in force (eV Angst^-1): 0.179448
Error in stress (kB): 3.180711
Bayesian error (eV Angst-1): 0.023225 0.000000
Spilling factor (-): 0.000368 0.020000
====================================================================================================
We see that for higher values of the weight the energy is still getting more accurate but the forces and stress are getting loosing accuracy at a higher, such that the overall error gets worse. We advise to use the optimal value.
If needed this waiting can be done in a similar way for the forces and stress.
Production runs using the optimized parameters
The production runs using the optimized parameters are run as normal calculations only using an additional line for the weight on energy. We repeat here which steps have to be performed:
- Copy CONTCAR to POSCAR if needed.
- Copy ML_ABNCAR to ML_ABCAR.
- Copy ML_FFNCAR to ML_FFCAR.
- Modify INCAR file:
- Set ML_FF_ISTART=2.
- Set ML_FF_WTOTEN=2.5.
- Set necessary molecular dynamics parameters (like e.g. NSW etc.).
User task: Calculate the pair correlation function as above with and without machine learning starting from the same POSCAR and compare the results.