Machine learning force field: Theory

Here we present the theory for on-the-fly machine learning force fields. The theory will be presented in a very condensed manner and for a more detailed description of the methods we refer the readers to Refs. , and .

Introduction

Molecular dynamics is one of the most important methods for the determination of dynamic properties. The quality of the molecular dynamics simulation depends very strongly on the accuracy of the calculational method, but higher accuracy usually comes at the cost of increased computational demand. A very accurate method is ab initio molecular dynamics, where the interactions of atoms and electrons are calculated fully quantum mechanically from ab initio calculations (such as e.g. DFT). Unfortunately this method is very often limited to small simulation cells and simulation times. One way to hugely speed up these calculations is by using force fields, which are parametrizations of the potential energy. These parametrizations can range frome very simple functions with only empirical parameters, to very complex functions parametrized using thousands of ab initio calculations. Usually making accurate force fields manually is a very time consuming task that needs tremendous expertise and know how.

Another way to greatly reduce computational cost and required human intervention is by machine learning. Here, in the prediction of the target property the method automatically interpolates between known training systems which were previously calculated by ab initio. This way the generation of force fields is already significantly simplified compared to classical force field which need manual (or even empirical) adjustment of the parameters. Nevertheless there is still the problem how to choose the proper (minimal) training data. One very efficient and automic way to solve that is to adapt on-the-fly learning. Here an MD calculation is used for the learning. During the run of the MD calculation ab initio data is picked out and added to the training data. From the existing data a force field is continuously built up. At each step it is judged whether to make an ab initio calculation and possibly add the data to the force field or to use the force field for that step and actually skip learning for that step. Hence the name "on the fly" learning. The crucial point here is the probability model for the estimation of errors. This model not force field is build up from newly sampled data. Hence, the more accurate the force field gets the less sampling is needed and the more expensive ab initio steps are skipped. This way not only the convergence of the force field can be controlled but also a very wide spread scan through phase space for the training structures can be performed. The crucial point for an on-the-fly machine learning which will be explained with the rest of the methodology in the following subsections, is to be able to predict errors of the force field on a newly sampled structure without the necessity to perform an ab initio calculation on that structure.

Algorithm

Fig. 1: On-the-fly machine learning force field generation scheme.

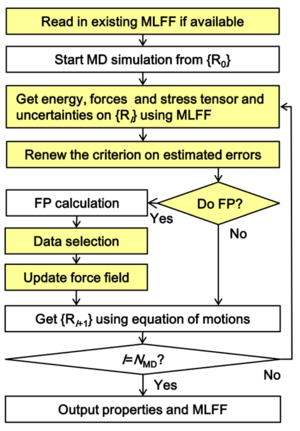
To obtain the machine-learning force field several structure datasets are required. A structure dataset defines the Bravais lattice and the atomic positions of the system and contains the total energy, the forces and the stress tensor calculated by first principles. Given these structure datasets, the machine identifies local configurations around an atom to learn what force field is appropriate. The local configuration measures the radial and angular distribution of neighboring atoms around this given site and is captured in so called descriptors.

The on-the-fly force field generation scheme is given by the following steps (a flowchart of the algorithm is shown in Fig. 1):

1. The machine predicts the energy, the forces and the stress tensor and their uncertainties for a given structure using the existing force field.
2. The machine decides whether to perform a first principles calculation (proceed with step 3); otherwise we skip to step 5.
3. Performing the first principles calculation, we obtain a new structure dataset which may improve the force field.
4. If the number of newly collected structures reaches a certain threshold or if the predicted uncertainty becomes too large, the machine learns an improved force field by including the new structure datasets and local configurations.
5. Atomic positions and velocities are updated by using the force field (if accurate enough) or the first principles calculation.
6. If the desired total number of ionic steps (NSW) is reached we are done; otherwise proceed with step 1.

Local energies

The potential energy $U$ of a structure with $N_{a}$ atoms is approximated as

$U=\sum \limits _{i=1}^{N_{\mathrm {a} }}U_{i}.$

The local energies $U_{i}$ are functionals $U_{i}=F[\rho _{i}(\mathbf {r} )]$ of the probability density $\rho _{i}$ to find another atom $j$ at the position $\mathbf {r}$ around the atom $i$ within a cut-off radius $R_{\mathrm {cut} }$ defined as

$\rho _{i}\left(\mathbf {r} \right)=\sum \limits _{j=1}^{N_{\mathrm {a} }}f_{\mathrm {cut} }\left(r_{ij}\right)g\left(\mathbf {r} -\mathbf {r} _{ij}\right),\qquad \qquad \qquad \qquad r_{ij}=|\mathbf {r} _{ij}|=|\mathbf {r} _{j}-\mathbf {r} _{i}|.$

Here $f_{\mathrm {cut} }$ is a cut-off function acting outside of $R_{\mathrm {cut} }$ and $g\left(\mathbf {r} -\mathbf {r} _{ij}\right)$ is a delta function.

The atom distribution can be also be written as a sum of individual distributions

$\rho _{i}\left(\mathbf {r} \right)=\sum \limits _{j\neq i}^{N_{\mathrm {a} }}\rho _{ij}\left(\mathbf {r} \right).$

Here $\rho _{ij}\left(\mathbf {r} \right)$ describes the probability of find an atom $j$ at a position $\mathbf {r}$ with respect to atom $i$.

Descriptors

Similar to the Smooth Overlap of Atomic Positions (SOAP) method the delta function $g(\mathbf {r} )$ is approximated as

$g\left(\mathbf {r} \right)={\frac {1}{\sqrt {2\sigma _{\mathrm {atom} }\pi }}}\mathrm {exp} \left(-{\frac {|\mathbf {r} |^{2}}{2\sigma _{\mathrm {atom} }^{2}}}\right).$

Fig. 2: Radial and angular descriptors.

Unfortunately $\rho _{i}\left(\mathbf {r} \right)$ is not rotationally invariant. To deal with this problem intermediate functions or descriptors depending on $\rho _{i}\left(\mathbf {r} \right)$ possessing rotational invariance are introduced:

Radial descriptor

This is the simplest descriptor which relies on the radial distribution function

$\rho _{i}^{(2)}\left(r\right)={\frac {1}{4\pi }}\int \rho _{i}\left(r{\hat {\mathbf {r} }}\right)d{\hat {\mathbf {r} }},$

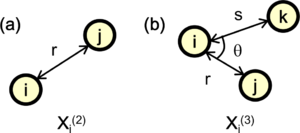
where ${\hat {\mathbf {r} }}$ denotes the unit vector of the vector $\mathbf {r}$ between atoms $i$ and $j$ [see Fig. 2 (a)]. The Radial descriptor can also be regarded as a two-body descriptor.

Angular descriptor

In most cases the radial descriptor is not enough to distinguish different probability densities $\rho _{i}$, since two different $\rho _{i}$ can yield the same $\rho _{i}^{(2)}$. To improve on this angular information between two radial descriptors is also incorporated within an angular descriptor

$\rho _{i}^{(3)}\left(r,s,\theta \right)=\iint d{\hat {\mathbf {r} }}d{\hat {\mathbf {s} }}\delta \left({\hat {\mathbf {r} }}\cdot {\hat {\mathbf {s} }}-\mathrm {cos} \theta \right)\sum \limits _{j=1}^{N_{a}}\sum \limits _{k\neq j}^{N_{a}}\rho _{ik}\left(r{\hat {\mathbf {r} }}\right)\rho _{ij}\left(s{\hat {\mathbf {s} }}\right)$

where $\theta$ denotes the angle between two vectors $\mathbf {r} _{ij}$ and $\mathbf {r} _{ik}$ [see Fig. 2 (b)]. The important difference of the function $\rho _{i}^{(3)}$ compared to the angular distribution function (also called power spectrum within the Gaussian Approximation Potential) used in reference is that no self interaction is included, where $j$ and $k$ have the same distance from $i$ and the angle between the two is zero. It can be shown that the self-interaction component are equivalent to the two body descriptor. This means that our angular descriptor is a pure angular descriptor, containing no two-body components and it cannot be expressed as linear combinations of the power spectrum. The advantage of this descriptor is that it enables us to separately control the effects of two- and three-body descriptors.

Basis set expansion

The atomic probability density can be also expanded in terms of basis functions

$\rho _{i}\left(\mathbf {r} \right)=\sum \limits _{l=1}^{L_{\mathrm {max} }}\sum \limits _{m=-l}^{l}\sum \limits _{n=1}^{N_{\mathrm {R} }^{l}}c_{nlm}^{i}\chi _{nl}\left(r\right)Y_{lm}\left({\hat {\mathbf {r} }}\right),$

where $c_{nlm}^{i}$, $\chi _{nl}$ and $Y_{lm}$ denote expansion coefficients, radial basis functions and spherical harmonics, respectively. The indices $n$, $l$ and $m$ denote radial numbers, angular and magnetic quantum numbers, respectively.

By using the above equation the radial descriptor and angular descriptor (power spectrum) can be written as

$\rho _{i}^{(2)}\left(r\right)={\frac {1}{\sqrt {4\pi }}}\sum \limits _{n=1}^{N_{\mathrm {R} }^{0}}c_{n00}^{i}\chi _{nl}\left(r\right),$

and

$\rho _{i}^{(3)}\left(r,s,\theta \right)=\sum \limits _{l=1}^{L_{\mathrm {max} }}\sum \limits _{n=1}^{N_{\mathrm {R} }^{l}}\sum \limits _{\nu =1}^{N_{\mathrm {R} }^{l}}{\sqrt {\frac {2l+1}{2}}}p_{n\nu l}^{i}\chi _{nl}\left(r\right)\chi _{\nu l}\left(s\right)P_{l}\left(\mathrm {cos} \theta \right),$

where $\chi _{\nu l}$ and $P_{l}$ represent normalized spherical Bessel functions and Legendre polynomials of order $l$.

The expansion coefficients for the angular descriptor can be converted to

$p_{n\nu l}^{i}={\sqrt {\frac {8\pi ^{2}}{2l+1}}}\sum \limits _{m=-l}^{l}\left[c_{nlm}^{i}c_{\nu lm}^{i*}-c_{nlm}^{ij}c_{\nu lm}^{ij*}\right],$

where $c_{nlm}^{ij}$ denotes expansion coefficients of the distribution $\rho _{ij}(\mathbf {r} )$ with respect to $\chi _{\nu l}$ and $P_{l}$

$\rho _{ij}(\mathbf {r} )=\sum \limits _{l=1}^{L_{\mathrm {max} }}\sum \limits _{m=-l}^{l}\sum \limits _{n=1}^{N_{\mathrm {R} }^{l}}c_{nlm}^{ij}\chi _{nl}\left(r\right)Y_{lm}\left({\hat {\mathbf {r} }}\right)$

and

$c_{nlm}^{i}=\sum \limits _{j}^{N_{a}}c_{nlm}^{ij}.$

In many cases $\chi _{nl}$ is multiplied with an angular filtering function $\eta$ (ML_FF_IAFILT2_MB), which can noticably reduce the necessary basis set size without losing accuracy in the calculations

$\eta _{l,a_{\mathrm {FILT} }}={\frac {1}{1+a_{\mathrm {FILT} }[l(l+1)]^{2}}}$

where $a_{\mathrm {FILT} }$ (ML_FF_AFILT2_MB) is a paramater controling the extent of the filtering. A larger value for the parameter should provide more filtering.

Potential energy fitting

It is convenient to express the local potential energy of atom $i$ in structure $\alpha$ in terms of linear coefficients $w_{i_{\mathrm {B} }}$ and a kernel $K\left(\mathbf {X} _{i},\mathbf {X} _{i_{\mathrm {B} }}\right)$ as follows

$U_{i}^{\alpha }=\sum \limits _{i_{\mathrm {B} }=1}^{N_{\mathrm {B} }}w_{i_{\mathrm {B} }}K\left(\mathbf {X} _{i}^{\alpha },\mathbf {X} _{i_{\mathrm {B} }}\right)$

where $N_{\mathrm {B} }$ is the basis set size. The kernel $K\left(\mathbf {X} _{i},\mathbf {X} _{i_{\mathrm {B} }}\right)$ measures the similarity between a local configuration from the training set $\rho _{i}(\mathbf {r} )$ and basis set $\rho _{i_{\mathrm {B} }}(\mathbf {r} )$. Using the radial and angular descriptors it is written as

$K\left(\mathbf {X} _{i},\mathbf {X} _{i_{\mathrm {B} }}\right)=\left[\beta \mathbf {X} _{i}^{(2)}\cdot \mathbf {X} _{i_{\mathrm {B} }}^{(2)}+(1-\beta )\mathbf {\hat {X}} _{i}^{(3)}\cdot \mathbf {\hat {X}} _{i_{\mathrm {B} }}^{(3)}\right]^{\zeta }.$

Here the vectors $\mathbf {X} _{i}^{(2)}$ and $\mathbf {\hat {X}} _{i}^{(3)}$ contain all coefficients $c_{n00}^{i}$ and $p_{n\nu l}^{i}$, respectively. The notation $\mathbf {\hat {X}} _{i}^{(3)}$ indicates that it is a normalized vector of $\mathbf {X} _{i}^{(3)}$. The parameter $\beta$ (ML_FF_W1_MB) controls the weighting of the radial and angular terms, respectively. The parameter $\zeta$ (ML_FF_NHYP1_MB) controls the sharpness of the kernel and the order of the many-body interactions.

Matrix vector form of linear equations

Similarly to the energy $U_{i}^{\alpha }$the forces and the stress tensor are also described as linear functions of the coefficients $w_{i_{\mathrm {B} }}$. All three are fitted simultaneously which leads to following matrix-vector form

$\mathbf {Y} =\mathbf {\Phi } \mathbf {w}$

where $\mathbf {Y}$ is a super vector consisting of the sub vectors $\{\mathbf {y} ^{\alpha }|\alpha =1,...,N_{\mathrm {st} }\}$. Here each $\mathbf {y} ^{\alpha }$ contains the first principle energies per atom, forces and stress tensors for each structure $\alpha$. $N_{\mathrm {st} }$ denotes the total number of structures. The size of $\mathbf {Y}$ is $N_{\mathrm {st} }\times (1+3N_{a}^{\alpha }+6)$.

The matrix $\mathbf {\Phi }$ is also called as design matrix. The rows of this matrix are blocked for each structure $\alpha$, where the first line of each block consists of the kernel used to calculate the energy. The subsequent $3N_{a}^{\alpha }$ lines consist of the derivatives of the kernel with respect to the atomic coordinates used to calculate the forces. The final 6 lines within each structure consist of the derivatives of the kernel with respect to the unit cell coordinates used to calculate the stress tensor components. The overall size of $\mathbf {Y}$ is $N_{\mathrm {st} }\times (1+3N_{a}^{\alpha }+6)\times N_{\mathrm {B} }$ looking like as follows

$\mathbf {\Phi } ={\begin{bmatrix}\sum _{i}{\frac {1}{N_{\mathrm {a} }^{\alpha =1}}}K\left(\mathbf {X} _{i}^{\alpha =1},\mathbf {X} _{i_{\mathrm {B} }=1}\right)&\sum _{i}{\frac {1}{N_{\mathrm {a} }^{\alpha =1}}}K\left(\mathbf {X} _{i}^{\alpha =1},\mathbf {X} _{i_{\mathrm {B} }=2}\right)&\dots &\dots &\dots \\\sum _{i}\nabla _{x_{1}}K\left(\mathbf {X} _{i}^{\alpha =1},\mathbf {X} _{i_{\mathrm {B} }=1}\right)&\sum _{i}\nabla _{x_{1}}K\left(\mathbf {X} _{i}^{\alpha =1},\mathbf {X} _{i_{\mathrm {B} }=2}\right)&\dots &\dots &\dots \\\sum _{i}\nabla _{y_{1}}K\left(\mathbf {X} _{i}^{\alpha =1},\mathbf {X} _{i_{\mathrm {B} }=1}\right)&\sum _{i}\nabla _{y_{1}}K\left(\mathbf {X} _{i}^{\alpha =1},\mathbf {X} _{i_{\mathrm {B} }=2}\right)&\dots &\dots &\dots \\\sum _{i}\nabla _{z_{1}}K\left(\mathbf {X} _{i}^{\alpha =1},\mathbf {X} _{i_{\mathrm {B} }=1}\right)&\sum _{i}\nabla _{z_{1}}K\left(\mathbf {X} _{i}^{\alpha =1},\mathbf {X} _{i_{\mathrm {B} }=2}\right)&\dots &\dots &\dots \\\sum _{i}\nabla _{x_{2}}K\left(\mathbf {X} _{i}^{\alpha =1},\mathbf {X} _{i_{\mathrm {B} }=1}\right)&\sum _{i}\nabla _{x_{2}}K\left(\mathbf {X} _{i}^{\alpha =1},\mathbf {X} _{i_{\mathrm {B} }=2}\right)&\dots &\dots &\dots \\\sum _{i}\nabla _{y_{2}}K\left(\mathbf {X} _{i}^{\alpha =1},\mathbf {X} _{i_{\mathrm {B} }=1}\right)&\sum _{i}\nabla _{y_{2}}K\left(\mathbf {X} _{i}^{\alpha =1},\mathbf {X} _{i_{\mathrm {B} }=2}\right)&\dots &\dots &\dots \\\sum _{i}\nabla _{z_{2}}K\left(\mathbf {X} _{i}^{\alpha =1},\mathbf {X} _{i_{\mathrm {B} }=1}\right)&\sum _{i}\nabla _{z_{2}}K\left(\mathbf {X} _{i}^{\alpha =1},\mathbf {X} _{i_{\mathrm {B} }=2}\right)&\dots &\dots &\dots \\\ldots &\ldots &\dots &\dots &\dots \\\ldots &\ldots &\dots &\dots &\dots \\\ldots &\ldots &\dots &\dots &\dots \\\sum _{i}{\frac {1}{N_{\mathrm {a} }^{\alpha =2}}}K\left(\mathbf {X} _{i}^{\alpha =2},\mathbf {X} _{i_{\mathrm {B} }=1}\right)&\sum _{i}{\frac {1}{N_{\mathrm {a} }^{\alpha =2}}}K\left(\mathbf {X} _{i}^{\alpha =2},\mathbf {X} _{i_{\mathrm {B} }=2}\right)&\dots &\dots &\dots \\\sum _{i}\nabla _{x_{1}}K\left(\mathbf {X} _{i}^{\alpha =2},\mathbf {X} _{i_{\mathrm {B} }=1}\right)&\sum _{i}\nabla _{x_{1}}K\left(\mathbf {X} _{i}^{\alpha =2},\mathbf {X} _{i_{\mathrm {B} }=2}\right)&\dots &\dots &\dots \\\sum _{i}\nabla _{y_{1}}K\left(\mathbf {X} _{i}^{\alpha =2},\mathbf {X} _{i_{\mathrm {B} }=1}\right)&\sum _{i}\nabla _{y_{1}}K\left(\mathbf {X} _{i}^{\alpha =2},\mathbf {X} _{i_{\mathrm {B} }=2}\right)&\dots &\dots &\dots \\\sum _{i}\nabla _{z_{1}}K\left(\mathbf {X} _{i}^{\alpha =2},\mathbf {X} _{i_{\mathrm {B} }=1}\right)&\sum _{i}\nabla _{z_{1}}K\left(\mathbf {X} _{i}^{\alpha =2},\mathbf {X} _{i_{\mathrm {B} }=2}\right)&\dots &\dots &\dots \\\sum _{i}\nabla _{x_{2}}K\left(\mathbf {X} _{i}^{\alpha =2},\mathbf {X} _{i_{\mathrm {B} }=1}\right)&\sum _{i}\nabla _{x_{2}}K\left(\mathbf {X} _{i}^{\alpha =2},\mathbf {X} _{i_{\mathrm {B} }=2}\right)&\dots &\dots &\dots \\\sum _{i}\nabla _{y_{2}}K\left(\mathbf {X} _{i}^{\alpha =2},\mathbf {X} _{i_{\mathrm {B} }=1}\right)&\sum _{i}\nabla _{y_{2}}K\left(\mathbf {X} _{i}^{\alpha =2},\mathbf {X} _{i_{\mathrm {B} }=2}\right)&\dots &\dots &\dots \\\sum _{i}\nabla _{z_{2}}K\left(\mathbf {X} _{i}^{\alpha =2},\mathbf {X} _{i_{\mathrm {B} }=1}\right)&\sum _{i}\nabla _{z_{2}}K\left(\mathbf {X} _{i}^{\alpha =2},\mathbf {X} _{i_{\mathrm {B} }=2}\right)&\dots &\dots &\dots \\\ldots &\ldots &\dots &\dots &\dots \\\ldots &\ldots &\dots &\dots &\dots \\\ldots &\ldots &\dots &\dots &\dots \end{bmatrix}}.$

Bayesian error estimation

Ultimately for error prediction we want to get the maximized probability of observing a new structure $\mathbf {y}$ on basis of the training set $\mathbf {Y}$, which is denoted as $p\left(\mathbf {y} |\mathbf {Y} \right)$. For this we need to get from the error of the linear fitting coefficients $\mathbf {w}$ in the reproduction of the training data $p\left(\mathbf {w} |\mathbf {Y} \right)$ to $p\left(\mathbf {y} |\mathbf {Y} \right)$ which is explained in the following.

First we obtain $p\left(\mathbf {w} |\mathbf {Y} \right)$ from the Bayesian theorem

$p\left(\mathbf {w} |\mathbf {Y} \right)={\frac {p\left(\mathbf {Y} |\mathbf {w} \right)p\left(\mathbf {w} \right)}{p\left(\mathbf {Y} \right)}}$,

where we assume multivariate Gaussian distributions ${\mathcal {N}}$ for the likelihood function

$p\left(\mathbf {Y} |\mathbf {w} \right)={\mathcal {N}}\left(\mathbf {Y} |\mathbf {\Phi } \mathbf {w} ,\sigma _{\mathrm {v} }^{2}\mathbf {I} \right)$

and the (conjugate) prior

$p\left(\mathbf {w} \right)={\mathcal {N}}\left(\mathbf {w} |\mathbf {0} ,\sigma _{\mathrm {w} }^{2}\mathbf {I} \right).$

The parameters $\sigma _{\mathrm {w} }^{2}$ and $\sigma _{\mathrm {v} }^{2}$ need to be optimized to balance the accuracy and robustness of the force field (see below). The normalization is obtained by

$p\left(\mathbf {Y} \right)=\int p\left(\mathbf {Y} |\mathbf {w} \right)p\left(\mathbf {w} \right)d\mathbf {w} .$

Using the equations from above and the completing square method $p\left(\mathbf {w} |\mathbf {Y} \right)$ is obtained as follows

$p\left(\mathbf {w} |\mathbf {Y} \right)={\mathcal {N}}\left(\mathbf {w} |\mathbf {\bar {w}} ,\mathbf {\Sigma } \right).$

Since the prior and the likelood function are described by multivariate Gaussian distributions the posterior ${\mathcal {N}}\left(\mathbf {w} |\mathbf {\bar {w}} ,\mathbf {\Sigma } \right)$ describes a multivariate Gaussian written as

${\mathcal {N}}\left(\mathbf {w} |\mathbf {\bar {w}} ,\mathbf {\Sigma } \right)={\frac {1}{\sqrt {\left(2\pi \right)^{N_{\mathrm {B} }}\mathrm {det} \mathbf {\Sigma } }}}\mathrm {exp} \left[-{\frac {\left(\mathbf {w} -\mathbf {\bar {w}} \right)^{\mathrm {T} }\mathbf {\Sigma } ^{-1}\left(\mathbf {w} -\mathbf {\bar {w}} \right)}{2}}\right]$

where we use the following definitions for the center of the Guassian distribution $\mathbf {\bar {w}}$ and the covariance matrix $\mathbf {\Sigma }$

$\mathbf {\bar {w}} ={\frac {1}{\sigma _{\mathrm {v} }^{2}}}\mathbf {\Sigma } \mathbf {\Phi } ^{\mathrm {T} }\mathbf {Y} ,$

$\mathbf {\Sigma } ^{-1}={\frac {1}{\sigma _{\mathrm {w} }^{2}}}\mathbf {I} +{\frac {1}{\sigma _{\mathrm {v} }^{2}}}\mathbf {\Phi } ^{\mathrm {T} }\mathbf {\Phi } .$

By using the relation

$p\left(\mathbf {y} |\mathbf {Y} \right)=\int p\left(\mathbf {y} |\mathbf {w} \right)p\left(\mathbf {w} |\mathbf {Y} \right)d\mathbf {w}$

and the completing square method the distribution of $p\left(\mathbf {y} |\mathbf {Y} \right)$ is written as

$p\left(\mathbf {y} |\mathbf {Y} \right)={\mathcal {N}}\left(\mathbf {\phi } \mathbf {\bar {w}} ,\mathbf {\sigma } \right),$

$\mathbf {\sigma } =\sigma _{\mathrm {v} }^{2}\mathbf {I} +\mathbf {\phi } ^{\mathrm {T} }\mathbf {\Sigma } \mathbf {\phi } .$

Here $\mathbf {\phi }$ is similar to $\mathbf {\Phi }$ but only for the new structure $\mathbf {y}$.

The mean vector $\mathbf {\phi } \mathbf {\bar {w}}$ contains the results of the predictions on the dimensionless energy per atom, forces and stress tensor. The diagonal elements of $\mathbf {\sigma }$, which correspond to the variances of the predicted results, are used as the uncertainty in the prediction.

Finally to get the best results and to prevent overfitting the parameters $\sigma _{\mathrm {v} }^{2}$ and $\sigma _{\mathrm {w} }^{2}$ have to be optimized. To achieve this, we use the evidence approximation (also called as empirical bayes, 2 maximum likelihood or generalized maximum likelihood), which maximizes the evidence function (also called model evidence) defined as

$p\left(\mathbf {Y} |\sigma _{\mathrm {v} }^{2},\sigma _{\mathrm {w} }^{2}\right)=\left({\frac {1}{\sqrt {2\pi \sigma _{\mathrm {v} }^{2}}}}\right)^{M}\left({\frac {1}{\sqrt {2\pi \sigma _{\mathrm {w} }^{2}}}}\right)^{N_{\mathrm {B} }}\int \mathrm {exp} \left[-E\left(\mathbf {w} \right)\right]d\mathbf {w} ,$

$E\left(\mathbf {w} \right)={\frac {1}{2\sigma _{\mathrm {v} }^{2}}}||\mathbf {\Phi } \mathbf {w} -\mathbf {Y} ||^{2}+{\frac {1}{2\sigma _{\mathrm {w} }^{2}}}||\mathbf {w} ||^{2}.$

The function $p\left(\mathbf {Y} |\sigma _{\mathrm {v} }^{2},\sigma _{\mathrm {w} }^{2}\right)$ corresponds to the probability that the regression model with parameters $\sigma _{\mathrm {v} }^{2}$ and $\sigma _{\mathrm {w} }^{2}$ provides the reference data $\mathbf {Y}$. Hence the best fit is optimized by maximizing this probability. The maximization is carried out by simultaneously solving the following equations

$\sigma _{\mathrm {w} }^{2}={\frac {|\mathbf {\bar {w}} |^{2}}{\gamma }},$

$\sigma _{\mathrm {v} }^{2}={\frac {|\mathbf {T} -\mathbf {\phi } \mathbf {\bar {w}} |^{2}}{M-\gamma }},$

$\gamma =\sum \limits _{k=1}^{N_{\mathrm {B} }}{\frac {\lambda _{k}}{\lambda _{k}+1/\sigma _{\mathrm {w} }^{2}}}$

where $\lambda _{k}$ are the eigenvalues of the matrix $\mathbf {\Phi } ^{\mathrm {T} }\mathbf {\Phi } /\sigma _{\mathrm {v} }^{2}$.

Sparsification

Within the machine learning force field methods the sparsification of local reference configurations and the angular descriptors is supported. The sparsification of local reference configurations is by default used and the extent is mainly controlled by ML_FF_EPS_LOW. This is procedure is really important to avoid overcompleteness and to damp the acquisition of new configurations special cases. The sparsification of angular descriptors is by default not used and should be used very cautiously and only if it's necessary. The description of the usage of this feature is given in ML_FF_LSPARSDES_MB.

Sparsification of local reference configurations

We start by defining the similarity kernel for the local configurations with each other

$\mathbf {K} _{i_{B},j_{B}}=\mathbf {K} \left(\mathbf {X} _{iB},\mathbf {X} _{j_{\mathrm {B} }}\right).$

The CUR algorithm starts out from the diagonalization of this matrix

$\mathbf {U} ^{T}\mathbf {K} _{i_{B},j_{B}}\mathbf {U} =\mathbf {L} ={\textrm {diag}}(l_{1},l_{2},...,l_{N_{B}}),$

where $\mathbf {U}$ is an eigenvector matrix defined as

$\mathbf {U} =(\mathbf {u} _{1},\mathbf {u} _{2},...,\mathbf {u} _{N_{b}},$

$\mathbf {U} _{j}^{T}=(u_{1j},u_{2j},...,u_{N_{b}j}).$

Using these notations the $j$th column vector of the matrix $\mathbf {K} _{i_{B},j_{B}}$ is expressed as

$\mathbf {k} _{j}=\sum \limits _{\chi =1}^{N_{B}}(u_{j\chi }l_{\chi })\mathbf {u} _{\chi }.$

In contrast to the original CUR algorithm which was developed to efficiently select a few significant columns from $\mathbf {K} _{i_{B},j_{B}}$, in our algorithm we want to look for (few) insignificant local configurations and throw them away. In our algorithm we dispose of the columns of $\mathbf {K} _{i_{B},j_{B}}$ that are correlated with the $N_{\mathrm {low} }$ eigenvectors $u_{\chi }$ with the smalles eigenvalues $l_{\chi }$. The correlation is measured by the statistical leverage scoring measured for each column $j$ of $\mathbf {K} _{i_{B},j_{B}}$ as

$\omega _{j}={\frac {1}{N_{\mathrm {low} }}}\sum \limits _{\chi =1}^{N_{B}}\gamma _{\chi ,j},$

$\gamma _{\chi ,j}=\left\{{\begin{array}{cl}u_{j\chi }^{2}&\mathrm {if} \,\,l_{\chi }>\epsilon _{\mathrm {low} }\\0&\mathrm {otherwise} \end{array}}\right.,$

where $\epsilon _{\mathrm {low} }$ (see also ML_FF_EPS_LOW) is a threshold for the lowest eigenvalues.

Sparsification of angular descriptors

The sparsification of the angular descriptors is done in a similar manner as for the local reference configurations. We start by defining the $N_{D}\times N_{D}$ square matrx

$\mathbf {A} =\mathbf {X} \mathbf {X} ^{T}.$

Here $N_{D}$ denotes the number of angular descriptors given by

$N_{D}=\sum \limits _{l=1}^{L_{\mathrm {max} }}{\frac {1}{2}}N_{R}^{l}\left(N_{R}^{l}+1\right)\left(L_{\mathrm {max} }+1\right).$

In this equation the symmetry of the descriptors $\rho _{n\nu l}=\rho _{\nu nl}$ is already taken into account. The matrix $\mathbf {X}$ is constructed from the vectors of the angular descriptors $\left(\mathbf {x} _{1}^{(3)},\mathbf {x} _{2}^{(3)},...,\mathbf {N_{B}} \right)$. The matrix $\mathbf {X}$ has dimension $N_{D}\times N_{B}$ and the matrix product is done over the $N_{B}$ elements of the local configurations.

In analogy to the local configurations the $j$th element of the matrix $\mathbf {A}$ is written as

$\mathbf {a} _{j}=\sum \limits _{\chi =1}^{N_{D}}(u_{j\chi }l_{\chi })\mathbf {u_{\chi }} .$

Opposite to the sparsification of the local configuration and more in line with the original CUR method, the columns of matrix $\mathbf {A}$ are kept when they are strongly correlated to the $k$ (see also ML_FF_NRANK_SPARSDES_MB eigenvectors $u_{\chi }$ which have the largest eigenvalues $l_{\chi }$. The correlation of the eigenvalues is then measured via a leverage scoring

$\omega _{j}={\frac {1}{k}}\sum \limits _{\chi =1}^{k}u_{j\chi }^{2}.$

From the leverage scorings, the ones with the highest values are selected until the ratio of the selected descriptors to the total number of descriptors becomes a previosly selected value $x_{\mathrm {spars} }$ (see also ML_FF_RDES_SPARSDES_MB).

---