Wrap-around errors: Difference between revisions
No edit summary |
No edit summary |
||
| Line 1: | Line 1: | ||
'''Wrap-around errors''' arise if the [[FFT meshes| Fast Fourier transformation (FFT) meshes]] are not | |||
Wrap around errors arise if the FFT meshes are not | |||
sufficiently large. It can be shown that no errors exist | sufficiently large. It can be shown that no errors exist | ||
if the FFT meshes contain all <math>\mathbf{G}</math> vectors up to <math>2 G_{\rm cut}</math>. | if the [[FFT meshes]] contain all <math>\mathbf{G}</math> vectors up to <math>2 G_{\rm cut}</math>. | ||
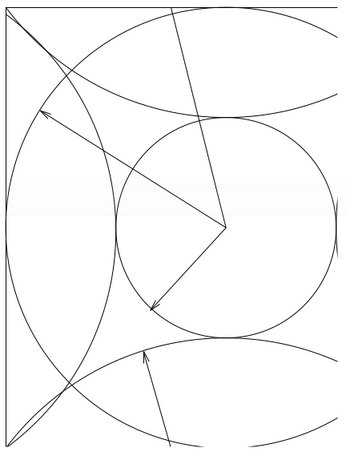
[[File:Wrap errors spheres.png|350px|thumb|Fig. 1: Sphere intersections for <math>G_{\mathrm{cut}}</math>]] | [[File:Wrap errors spheres.png|350px|thumb|Fig. 1: Sphere intersections for <math>G_{\mathrm{cut}}</math>]] | ||
| Line 12: | Line 11: | ||
The wavefunction is defined as | The wavefunction is defined as | ||
<math> | ::<math> | ||
| \phi_{n\mathbf{k}} \rangle = \sum_\mathbf{G} C_{\mathbf{G}n\mathbf{k}} | \mathbf{k}+\mathbf{G}\rangle, | | \phi_{n\mathbf{k}} \rangle = \sum_\mathbf{G} C_{\mathbf{G}n\mathbf{k}} | \mathbf{k}+\mathbf{G}\rangle, | ||
</math> | </math> | ||
| Line 18: | Line 17: | ||
and in real space it is given by | and in real space it is given by | ||
<math> | ::<math> | ||
\langle \mathbf{r}| \phi_{n\mathbf{k}} \rangle = \sum_\mathbf{G} \langle \mathbf{r}| \mathbf{k}+\mathbf{G}\rangle \langle \mathbf{k}+\mathbf{G}|\phi_{n\mathbf{k}} \rangle | \langle \mathbf{r}| \phi_{n\mathbf{k}} \rangle = \sum_\mathbf{G} \langle \mathbf{r}| \mathbf{k}+\mathbf{G}\rangle \langle \mathbf{k}+\mathbf{G}|\phi_{n\mathbf{k}} \rangle | ||
= \frac{1}{\Omega^{1/2}} \sum_\mathbf{G} e^{i(\mathbf{k}+\mathbf{G})\mathbf{r}} C_{\mathbf{G}n\mathbf{k}}. | = \frac{1}{\Omega^{1/2}} \sum_\mathbf{G} e^{i(\mathbf{k}+\mathbf{G})\mathbf{r}} C_{\mathbf{G}n\mathbf{k}}. | ||
</math> | </math> | ||
Using | Using FFTs one can define | ||
<math> | ::<math> | ||
C_{\mathbf{r}n\mathbf{k}}= \sum_{\mathbf{G}} C_{\mathbf{G}n\mathbf{k}} e^{i\mathbf{G} \mathbf{r}} \qquad \qquad \qquad | C_{\mathbf{r}n\mathbf{k}}= \sum_{\mathbf{G}} C_{\mathbf{G}n\mathbf{k}} e^{i\mathbf{G} \mathbf{r}} \qquad \qquad \qquad | ||
C_{\mathbf{G}n\mathbf{k}}= \frac{1}{N_{\mathrm{FFT}}} \sum_{\mathbf{r}} C_{\mathbf{r}n\mathbf{k}} e^{-i\mathbf{G} \mathbf{r}}. | C_{\mathbf{G}n\mathbf{k}}= \frac{1}{N_{\mathrm{FFT}}} \sum_{\mathbf{r}} C_{\mathbf{r}n\mathbf{k}} e^{-i\mathbf{G} \mathbf{r}}. | ||
| Line 32: | Line 31: | ||
Therefore the wavefunction can be written in real space as | Therefore the wavefunction can be written in real space as | ||
<math> | ::<math> | ||
\langle\mathbf{r}| \phi_{n\mathbf{k}} \rangle = \phi_{n\mathbf{k}}(r) = \frac{1}{\Omega^{1/2}} C_{\mathbf{r}n\mathbf{k}} e^{i\mathbf{k}\mathbf{r}}. | \langle\mathbf{r}| \phi_{n\mathbf{k}} \rangle = \phi_{n\mathbf{k}}(r) = \frac{1}{\Omega^{1/2}} C_{\mathbf{r}n\mathbf{k}} e^{i\mathbf{k}\mathbf{r}}. | ||
</math> | </math> | ||
| Line 38: | Line 37: | ||
The charge density is simply given by | The charge density is simply given by | ||
<math> | ::<math> | ||
\rho^{\mathrm{ps}}_{\mathbf{r}} \equiv \langle \mathbf{r} |\rho^{\mathrm{ps}} | \mathbf{r} \rangle = | \rho^{\mathrm{ps}}_{\mathbf{r}} \equiv \langle \mathbf{r} |\rho^{\mathrm{ps}} | \mathbf{r} \rangle = | ||
\sum_\mathbf{k} w_{\mathbf{k}} \sum_n f_{n\mathbf{k}} \phi_{n\mathbf{k}}(r) \phi^{*}_{n\mathbf{k}}(r) , | \sum_\mathbf{k} w_{\mathbf{k}} \sum_n f_{n\mathbf{k}} \phi_{n\mathbf{k}}(r) \phi^{*}_{n\mathbf{k}}(r) , | ||
| Line 45: | Line 44: | ||
and in the reciprocal mesh it can be written as | and in the reciprocal mesh it can be written as | ||
<math> | ::<math> | ||
\rho^{\mathrm{ps}}_\mathbf{G} \equiv | \rho^{\mathrm{ps}}_\mathbf{G} \equiv | ||
\frac{1}{\Omega} \int \langle\mathbf{r} | \rho^{\mathrm{ps}}| \mathbf{r}\rangle e^{-i \mathbf{G}\mathbf{r}}\, d \mathbf{r} \to \frac{1}{N_{\mathrm{FFT}}} \sum_{\mathbf{r}} \rho^{\mathrm{ps}}_{\mathbf{r}} e^{-i \mathbf{G}\mathbf{r}}. | \frac{1}{\Omega} \int \langle\mathbf{r} | \rho^{\mathrm{ps}}| \mathbf{r}\rangle e^{-i \mathbf{G}\mathbf{r}}\, d \mathbf{r} \to \frac{1}{N_{\mathrm{FFT}}} \sum_{\mathbf{r}} \rho^{\mathrm{ps}}_{\mathbf{r}} e^{-i \mathbf{G}\mathbf{r}}. | ||
| Line 64: | Line 63: | ||
calculated. The action of the local-potential is given by | calculated. The action of the local-potential is given by | ||
<math> | ::<math> | ||
a_{\mathbf{r}} = V_{\mathbf{r}} C_{\mathbf{r}n\mathbf{k}}. | a_{\mathbf{r}} = V_{\mathbf{r}} C_{\mathbf{r}n\mathbf{k}}. | ||
</math> | </math> | ||
| Line 76: | Line 75: | ||
<math>2 G_{\mathrm{cut}}</math>). | <math>2 G_{\mathrm{cut}}</math>). | ||
If the FFT | If the FFT mesh contains all components up to <math>2 G_{\mathrm cut}</math> | ||
the resulting wrap-around error is once again 0. This can | the resulting wrap-around error is once again 0. This can | ||
be easily seen in Fig. 1. Here we see that the small sphere contains all plane waves included in the basis set <math>G<G_{\mathrm{cut}}</math>. | be easily seen in Fig. 1. Here we see that the small sphere contains all plane waves included in the basis set <math>G<G_{\mathrm{cut}}</math>. | ||
The charge density contains components up to <math>2 G_{\mathrm{cut}}</math> (second sphere), and | The charge density contains components up to <math>2 G_{\mathrm{cut}}</math> (second sphere), and | ||
the acceleration <math>a</math> components up to <math>3 G_{\mathrm{cut}}</math>, which are reflected | the acceleration <math>a</math> components up to <math>3 G_{\mathrm{cut}}</math>, which are reflected | ||
in (third sphere) because of the finite size of the FFT | in (third sphere) because of the finite size of the FFT mesh. Nevertheless | ||
the components <math>a_{\mathbf{G}}</math> with <math>| \mathbf{G}| < G_{\mathrm{cut}}</math> are correct i.e. | the components <math>a_{\mathbf{G}}</math> with <math>| \mathbf{G}| < G_{\mathrm{cut}}</math> are correct i.e. | ||
the small sphere does not intersect with the third large sphere} | the small sphere does not intersect with the third large sphere} | ||
| Line 90: | Line 89: | ||
{{TAG|NGX}}, | {{TAG|NGX}}, | ||
{{TAG|NGY}}, | {{TAG|NGY}}, | ||
{{TAG|NGZ}} | {{TAG|NGZ}} | ||
[[ | |||
[[Energy cutoff and FFT meshes]] | |||
[[Category:Electronic minimization]][[Category:Charge density]][[Category:Theory]] | [[Category:Electronic minimization]][[Category:Charge density]][[Category:Theory]] | ||
Latest revision as of 09:00, 24 October 2025
Wrap-around errors arise if the Fast Fourier transformation (FFT) meshes are not sufficiently large. It can be shown that no errors exist if the FFT meshes contain all [math]\displaystyle{ \mathbf{G} }[/math] vectors up to [math]\displaystyle{ 2 G_{\rm cut} }[/math].
It can be shown that the charge density contains components up to [math]\displaystyle{ 2 G_{\mathrm{cut}} }[/math], where [math]\displaystyle{ 2 G_{\mathrm{cut}} }[/math] is the "longest" plane wave in the basis set:
The wavefunction is defined as
- [math]\displaystyle{ | \phi_{n\mathbf{k}} \rangle = \sum_\mathbf{G} C_{\mathbf{G}n\mathbf{k}} | \mathbf{k}+\mathbf{G}\rangle, }[/math]
and in real space it is given by
- [math]\displaystyle{ \langle \mathbf{r}| \phi_{n\mathbf{k}} \rangle = \sum_\mathbf{G} \langle \mathbf{r}| \mathbf{k}+\mathbf{G}\rangle \langle \mathbf{k}+\mathbf{G}|\phi_{n\mathbf{k}} \rangle = \frac{1}{\Omega^{1/2}} \sum_\mathbf{G} e^{i(\mathbf{k}+\mathbf{G})\mathbf{r}} C_{\mathbf{G}n\mathbf{k}}. }[/math]
Using FFTs one can define
- [math]\displaystyle{ C_{\mathbf{r}n\mathbf{k}}= \sum_{\mathbf{G}} C_{\mathbf{G}n\mathbf{k}} e^{i\mathbf{G} \mathbf{r}} \qquad \qquad \qquad C_{\mathbf{G}n\mathbf{k}}= \frac{1}{N_{\mathrm{FFT}}} \sum_{\mathbf{r}} C_{\mathbf{r}n\mathbf{k}} e^{-i\mathbf{G} \mathbf{r}}. }[/math]
Therefore the wavefunction can be written in real space as
- [math]\displaystyle{ \langle\mathbf{r}| \phi_{n\mathbf{k}} \rangle = \phi_{n\mathbf{k}}(r) = \frac{1}{\Omega^{1/2}} C_{\mathbf{r}n\mathbf{k}} e^{i\mathbf{k}\mathbf{r}}. }[/math]
The charge density is simply given by
- [math]\displaystyle{ \rho^{\mathrm{ps}}_{\mathbf{r}} \equiv \langle \mathbf{r} |\rho^{\mathrm{ps}} | \mathbf{r} \rangle = \sum_\mathbf{k} w_{\mathbf{k}} \sum_n f_{n\mathbf{k}} \phi_{n\mathbf{k}}(r) \phi^{*}_{n\mathbf{k}}(r) , }[/math]
and in the reciprocal mesh it can be written as
- [math]\displaystyle{ \rho^{\mathrm{ps}}_\mathbf{G} \equiv \frac{1}{\Omega} \int \langle\mathbf{r} | \rho^{\mathrm{ps}}| \mathbf{r}\rangle e^{-i \mathbf{G}\mathbf{r}}\, d \mathbf{r} \to \frac{1}{N_{\mathrm{FFT}}} \sum_{\mathbf{r}} \rho^{\mathrm{ps}}_{\mathbf{r}} e^{-i \mathbf{G}\mathbf{r}}. }[/math]
Using the above equations for [math]\displaystyle{ \rho^{\mathrm{ps}}_{\mathbf{r}} }[/math] and [math]\displaystyle{ C_{\mathbf{r}n\mathbf{k}} }[/math] it is very easy to show that [math]\displaystyle{ \rho^{\mathrm{ps}}_{\mathbf{r}} }[/math] contains Fourier-components up to [math]\displaystyle{ 2 G_{\mathrm{cut}} }[/math].
Generally it can be shown that a the convolution [math]\displaystyle{ f_r=f^1_r f^2_r }[/math] of two functions [math]\displaystyle{ f^1_r }[/math] with Fourier-components up to [math]\displaystyle{ G_1 }[/math] and [math]\displaystyle{ f^2_r }[/math] with Fourier-components up to [math]\displaystyle{ G_2 }[/math] contains Fourier-components up to [math]\displaystyle{ G_1+G_2 }[/math].
The property of the convolution comes once again into play, when the action of the Hamiltonian onto a wavefunction is calculated. The action of the local-potential is given by
- [math]\displaystyle{ a_{\mathbf{r}} = V_{\mathbf{r}} C_{\mathbf{r}n\mathbf{k}}. }[/math]
Only the components [math]\displaystyle{ a_{\mathbf{G}} }[/math] with [math]\displaystyle{ |\mathbf{G}| \lt G_{\mathrm{cut}} }[/math] are taken into account (see section ALGO: [math]\displaystyle{ a_{\mathbf{G}} }[/math] is added to the wavefunction during the iterative refinement of the wavefunctions [math]\displaystyle{ C_{\mathbf{G}n\mathbf{k}} }[/math], and [math]\displaystyle{ C_{\mathbf{G}n\mathbf{k}} }[/math] contains only components up to [math]\displaystyle{ G_{\mathrm{cut}} }[/math]). From the previous theorem we see that [math]\displaystyle{ a_{\mathbf{r}} }[/math] contains components up to [math]\displaystyle{ 3 G_{\mathrm{cut}} }[/math] ([math]\displaystyle{ V_{\mathbf{r}} }[/math] contains components up to [math]\displaystyle{ 2 G_{\mathrm{cut}} }[/math]).
If the FFT mesh contains all components up to [math]\displaystyle{ 2 G_{\mathrm cut} }[/math] the resulting wrap-around error is once again 0. This can be easily seen in Fig. 1. Here we see that the small sphere contains all plane waves included in the basis set [math]\displaystyle{ G\lt G_{\mathrm{cut}} }[/math]. The charge density contains components up to [math]\displaystyle{ 2 G_{\mathrm{cut}} }[/math] (second sphere), and the acceleration [math]\displaystyle{ a }[/math] components up to [math]\displaystyle{ 3 G_{\mathrm{cut}} }[/math], which are reflected in (third sphere) because of the finite size of the FFT mesh. Nevertheless the components [math]\displaystyle{ a_{\mathbf{G}} }[/math] with [math]\displaystyle{ | \mathbf{G}| \lt G_{\mathrm{cut}} }[/math] are correct i.e. the small sphere does not intersect with the third large sphere}
