RPA/ACFDT: Correlation energy in the Random Phase Approximation
ACFDT stands for the adiabatic connection fluctuation dissipation theorem and is an alternative way to derive the energy expression for the correlation energy in the random phase approximation (RPA). In the following, the diagrammatic description is presented. For the ACFDT formulation, the reader is referred to the literature.[1] There is also a lecture introducing RPA on our YouTube channel.
Diagrammatic approach to the correlation energy
The correlation energy is defined as the missing piece of the Hartree-Fock energy to the total energy, that is . The exact form of is unknown and can be calculated only approximately for a realistic system. The Random Phase Approximation (RPA) is such an approximation that provides access to . The RPA was first studied by Bohm and Pines for the homogeneous electron gas and was later recognized by Gell-Mann and Brueckner as an approximation of that can be expressed in the same language as Feynman used a few years earlier to describe the positron. [2][3][4]
Feynman's diagrammatic approach is based on quantum field theory (QFT), which in turn is based on the Gell-Mann and Low theorem. This theorem states that the eigenstate of an interacting Hamiltonian can be expressed in terms of the eigenstates of the non-interacting one.[5] For this reason, each diagrammatic calculation, like the RPA or GW, requires the solution of the non-interacting Hamiltonian of the system, like for instance the Hartree-Fock energies and orbitals or the solutions of the Kohn-Sham Hamiltonian .
QFT is commonly formulated in the Dirac (also known as interaction) picture, where dynamics described by the interaction part of the fully interacting Hamiltonian are singled out via time-dependent operators like . These operators act on states like the non-interacting groundstate of the system causing fluctuations at a specific point in time. The main idea of QFT is to understand observations, which can be measured by an observer, as a collective phenomenon of all possible fluctuations.[6]
Thereby, fluctuations are understood as the creation of virtual electrons (and holes) that interact with each other and are annihilated after some time. Formally this is achieved by introducing creation and annihilation operators that satisfy following relations
The first relation defines the non-interacting groundstate as the Fermi vacuum (the groundstate in the absence of any fluctuations), while the second and third anti-commutator relations are a consequence of the Pauli principle. In fact, all operators that describe measurable quantities of a system of interacting electrons can be represented in terms of and alone; additional objects are not necessary.
However, the time-ordering operator
where is the unit step function, and the time-evolution operator
are helpful quantities, since they allow to formulate the Gell-Mann and Low theorem as follows.
Gell-Mann and Low theorem
Using adiabatic coupling of the interaction , Gell-Mann and Low proved that the vectors
are the eigenstates of the interacting Hamiltonian.[5]
We follow the common literature and suppress the infinitesimal in the following bearing in mind that the limit is performed at the very end of the calculation.[7][8]
Diagrammatic perturbation theory
A consequence of the Gell-Mann and Low theorem, is the following form of the interacting groundstate energy[8]
which can be seen as starting point of diagrammatic perturbation theory. The expression above is used to derive all possible approximations by expanding the time-evolution operator into a series. The resulting matrix-elements of creation and annihilation operators are evaluated term by term using the canonical anti-commutator relations defined above (Wick's theorem[9]). It follows that all terms in perturbation theory are expressed by only two quantities, the non-interacting Feynman propagator
and the Coulomb interaction
Then, each term in the series corresponds to an integral over space-time coordinates .
Feynman diagrams are used to illustrate which terms are considered in the perturbation series. The illustration is usually achieved with so-called Feynman rules that map a specific diagram to an integral (and vice versa). For instance the second order diagram
is also known as the direct Møller-Plessett term and stands for following integral
All Feynman rules can be found in the book of Negele and Orland or elsewhere.[7][8]
The random-phase approximation
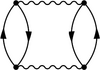
The RPA is obtained from neglecting all second and higher order terms in the perturbation series of the groundstate energy, except of those which can be expressed soley in terms of the independent particle polarizability
corresponding to the "bubble" diagram
Because of the symmetric time property , the independent particle polarizability is of bosonic character. Because the RPA neglects all non-bosonic terms in the perturbation series, it corresponds essentially to a "bosonization" of the many-body problem for which the n-th order term can be written analytically as[7]
Here, the trace of the matrix product is most effectively done in reciprocal space using the Fourier transformed polarizability , the diagonal Coulomb potential and the conserved crystal momentum in the first Brillouin zone.
All bubble terms of order can be written in a closed form using the series for the logarithm and define the correlation part of the RPA energy
There are two first order contributions to the total energy that yield the exact exchange energy , which is usually determined separately.
Computational Complexity
The calculation of the RPA integral requires the determination of the independent particle polarizability matrix on each of the sampling points of the first Brillouin zone for frequency points. The number of frequency points is reduced drastically, by performing the integration over the imaginary frequency axis .[10]
The independent particle polarizability on the imaginary axis can be determined with two alternative methods.
Quartic scaling RPA: Direct calculation
Direct calculation of using the formula of Adler and Wiser[11] [12]
yields an RPA algorithm that has a computational cost of . Because the number of plane waves scales linearly with the system size (number of electrons in the unit cell), the direct calculation of the polarizability is unfavourable for large system sizes, e.g. for more than ~20 atoms in the unit cell.
Cubic scaling RPA: Contraction of imaginary time Green's functions
An alternative way to determine is to frist determine imaginary time Green's functions of the form[13]
and to perform afterwards a Fourier transformation into reciprocal and imaginary frequency space of
Although more evolved, this approach has the advantage that the computational cost for the determination of scales with and is essentially only cubic in system size. The space-time method allows to study relatively large systems with the RPA.[14]
Basis set convergence of RPA-ACFDT calculations
The expression for the ACFDT-RPA correlation energy written in terms of reciprocal lattice vectors reads:
.
The sum over reciprocal lattice vectors has to be truncated at some , determined by < ENCUTGW, which can be set in the INCAR file. The default value is ENCUT, which experience has taught us not to change. For systematic convergence tests, instead increase ENCUT and repeat steps 1 to 4, but be aware that the "maximum number of plane-waves" changes when ENCUT is increased. Note that it is virtually impossible, to converge absolute correlation energies. Rather concentrate on relative energies (e.g. energy differences between two solids, or between a solid and the constituent atoms).
Since correlation energies converge very slowly with respect to , VASP automatically extrapolates to the infinite basis set limit using a linear regression to the equation: [1][15][16]
.
Furthermore, the Coulomb kernel is smoothly truncated between ENCUTGWSOFT and ENCUTGW using a simple cosine like window function (Hann window function). Alternatively, the basis set extrapolation can be performed by setting LSCK=.TRUE., using the squeezed Coulomb kernel method.[17]
The default for ENCUTGWSOFT is 0.8ENCUTGW (again we do not recommend to change this default).
The integral over is evaluated by means of a highly accurate minimax integration.[10] The number of points is determined by the flag NOMEGA, whereas the energy range of transitions is determined by the band gap and the energy difference between the lowest occupied and highest unoccupied one-electron orbital. VASP determines these values automatically (from vasp.5.4.1 on), and the user should only carefully converge with respect to the number of frequency points NOMEGA. A good choice is usually NOMEGA=12, however, for large gap systems one might obtain eV convergence per atom already using 8 points, whereas for metals up to NOMEGA=24 frequency points are sometimes necessary, in particular, for large unit cells.
Strictly adhere to the steps outlines above. Specifically, be aware that steps two and three require the WAVECAR file generated in step one, whereas step four requires the WAVECAR and WAVEDER file generated in step three (generated by setting LOPTICS=.TRUE.).
Matsubara Formalism: Metallic systems at finite Temperature
The zero-temperature formalism of many-body perturbation theory breaks down for metals (systems with zero energy band-gap) as pointed out by Kohn and Luttinger.[18] This conundrum is lifted by considering diagrammatic perturbation theory at finite temperature , which may be understood by an analytical continuation of the real-time to the imaginary time axis . Matsubara has shown that this Wick rotation in time reveals an intriguing connection to the inverse temperature of the system.[19] More precisely, Matsubara has shown that all terms in perturbation theory at finite temperature can be expressed as integrals of imaginary time quantities (such as the polarizability ) over the fundamental interval .
As a consequence, one decomposes imaginary time quantities into a Fourier series with period that determines the spacing of the Fourier modes. For instance the imaginary polarizability can be written as
and the corresponding random-phase approximation of the correlation energy at finite temperature becomes a series over (in this case, bosonic) Matsubara frequencies
The Matsubara formalism has the advantage that all contributions to the Green's function and the polarizability are mathematically well-defined, including contributions from states close to the chemical potential , such that Matsubara series also converge for metallic systems.
Although formally convenient, the Matsubara series converges poorly with the number of considered terms in practice. VASP, therefore, uses a compressed representation of the Fourier modes by employing the Minimax-Isometry method.[20] This approach converges exponentially with the number of considered frequency points.
References
- ↑ a b J. Harl and G. Kresse, Phys. Rev. B 77, 045136 (2008).
- ↑ D. Bohm and D. Pines, J. Phys. 82, 625 (1951).
- ↑ M. Gell-Mann and K. Brueckner, J. Phys. 106, 364 (1957).
- ↑ R. P. Feynman, J. Phys. 76, 749 (1948).
- ↑ a b M. Gell-Mann and F. Low, J. Phys. 84, 350 (1951).
- ↑ R. D. Mattuck, Dover Books on Physics (2012).
- ↑ a b c J. Negele and H. Orland, Frontiers in Physics (1988).
- ↑ a b c A. L. Fetter and J. D. Walecka, Dover Books on Physics (2003).
- ↑ G. C. Wick, Phys. Rev. 80, 268 (1950).
- ↑ a b M. Kaltak, J. Klimeš, and G. Kresse, J. Chem. Theory Comput. 10, 2498-2507 (2014).
- ↑ S. L. Adler, Phys. Rev. 126, 413 (1962)
- ↑ N. Wiser, Phys. Rev. 129, 62 (1963)
- ↑ H. N. Rojas, R. W. Godby, and R. J. Needs, Phys. Rev. Lett. 74, 1827 (1995).
- ↑ M. Kaltak, J. Klimeš, and G. Kresse, Phys. Rev. B 90, 054115 (2014).
- ↑ J. Harl, L. Schimka, and G. Kresse, Phys. Rev. B 81, 115126 (2010).
- ↑ J. Klimeš, M. Kaltak, and G. Kresse, Phys. Rev. B 90, 075125 (2014).
- ↑ S. Riemelmoser, M. Kaltak, and G. Kresse, JCP 152(13), 134103 (2020).
- ↑ W. Kohn and J. M. Luttinger, Phys. Rev. 118, 41 (1960).
- ↑ T. Matsubara, Prog. Theor. Phys. 14, 351 (1955).
- ↑ M. Kaltak and G. Kresse, Phys. Rev. B. 101, 205145 (2020).