FAQ
I can not compile the parallel version of VASP under LINUX?
Mind that VASP will generally not link correctly to mpi versions compiled with g77/f77, since g77/f77 append two underscores to external symbols already containing one underscore (i.e. MPI_SEND becomes mpi_send__). The portland group compiler however appends one underscore. Although the pgf90 compiler has an option to work around this problem, we yet faild to link against mpi libraries generated for g77/f77. Hence you must compile mpi (mpich and/or lam) yourself. This is really easy and simple, if the machine has been set up properly (have a look at our makefiles). If the compilation of mpich and/or lam fails, VASP will almost certainly not work in parallel on your machine, and we strongly urge you to reinstall LINUX.
Why is the cohesive energy much larger than reported in other papers?
Several reasons can be responsible for this:
First, VASP calculates the cohesive energy with respect to a spherical non spin-polarised atom. One should however calculate the cohesive energy with respect to a spin polarised atom. These corrections are usually called (atomic) spin-polarisation corrections, and they must be subtracted manually from the calculated cohesive energy calculated by VASP.
Second, many older calculations report too small cohesive energies, since basis sets were often insufficient. It is now well accepted that the local density approximation overestimates the cohesive energy significantly in many cases.
Which k-points should I use?
For metallic system, k-point convergence is usually a critical issue. There are a few general hints which might be helpfull:
- For hexagonal cells, Gamma centered k-point grids converge much faster than other grids. In fact, most meshes that do not include the [math]\displaystyle{ \Gamma }[/math] point break the symmetry of the hexagonal lattice! Even with increasing grid densities the wrong results might be obtained.
- Up to divisions of 8 (i.e. [math]\displaystyle{ 8\times8\times1 }[/math] for a surface) even Monkhorst Pack grids which do not contain the Gamma point, perform better than odd Monkhorst Pack grids (this does not apply to hexagonal cells, see above). In other words one obtains better converged results with even grids.
- For adsorbates on surfaces, it is sometimes feasable to use only the k-points of the high symmetry Brillouin zone, even if the adsorbate breaks the symmetry. These k-point grids can be generated by running VASP with a POSCAR for which all adatoms have been removed. The resulting IBZKPT file can be copied to KPOINTS. For convenicene, the following k-point grids can be used for hexagonal cells:
Gamma centered 2x2
Automatically generated mesh
2
Reciprocal lattice
0.00000000000000 0.00000000000000 0.00000000000000 1
0.50000000000000 0.00000000000000 0.00000000000000 3
Gamma centered 3x3
Automatically generated mesh
3
Reciprocal lattice
0.00000000000000 0.00000000000000 0.00000000000000 1
0.33333333333333 0.00000000000000 0.00000000000000 6
0.33333333333333 0.33333333333333 0.00000000000000 2
Gamma centered 4x4
Automatically generated mesh
4
Reciprocal lattice
0.00000000000000 0.00000000000000 0.00000000000000 1
0.25000000000000 0.00000000000000 0.00000000000000 6
0.50000000000000 0.00000000000000 0.00000000000000 3
0.25000000000000 0.25000000000000 0.00000000000000 6
Gamma centered 5x5
Automatically generated mesh
5
Reciprocal lattice
0.00000000000000 0.00000000000000 0.00000000000000 1
0.20000000000000 0.00000000000000 0.00000000000000 6
0.40000000000000 0.00000000000000 0.00000000000000 6
0.20000000000000 0.20000000000000 0.00000000000000 6
0.40000000000000 0.20000000000000 0.00000000000000 6
Gamma centered 6x6
Automatically generated mesh
7
Reciprocal lattice
0.00000000000000 0.00000000000000 0.00000000000000 1
0.16666666666667 0.00000000000000 0.00000000000000 6
0.33333333333333 0.00000000000000 0.00000000000000 6
0.50000000000000 0.00000000000000 0.00000000000000 3
0.16666666666667 0.16666666666667 0.00000000000000 6
0.33333333333333 0.16666666666667 0.00000000000000 12
0.33333333333333 0.33333333333333 0.00000000000000 2
For cubic surface cells, the following k-points can be used:
Monkhorst Pack: 2x2x1
1
Reciprocal lattice
0.25000000000000 0.25000000000000 0.00000000000000 4
Monkhorst Pack: 4x4x1
3
Reciprocal lattice
0.12500000000000 0.12500000000000 0.00000000000000 4
0.37500000000000 0.12500000000000 0.00000000000000 8
0.37500000000000 0.37500000000000 0.00000000000000 4
Monkhorst Pack: 6x6x1
6
Reciprocal lattice
0.08333333333333 0.08333333333333 0.00000000000000 4
0.25000000000000 0.08333333333333 0.00000000000000 8
0.41666666666667 0.08333333333333 0.00000000000000 8
0.25000000000000 0.25000000000000 0.00000000000000 4
0.41666666666667 0.25000000000000 0.00000000000000 8
Monkhorst Pack: 8x8x1
10
Reciprocal lattice
0.06250000000000 0.06250000000000 0.00000000000000 4
0.18750000000000 0.06250000000000 0.00000000000000 8
0.31250000000000 0.06250000000000 0.00000000000000 8
0.43750000000000 0.06250000000000 0.00000000000000 8
0.18750000000000 0.18750000000000 0.00000000000000 4
0.31250000000000 0.18750000000000 0.00000000000000 8
0.43750000000000 0.18750000000000 0.00000000000000 8
0.31250000000000 0.31250000000000 0.00000000000000 4
0.43750000000000 0.31250000000000 0.00000000000000 8
0.43750000000000 0.43750000000000 0.00000000000000 4
Question Why is convergence to the ionic groundstate so slow?
In general convergence depends on the eigenvalue spectrum of the Hessian matrix (second derivative of the energy with respect to positions). Roughly speaking the number of steps equals
[math]\displaystyle{ N = \sqrt{ \frac{ \epsilon_{\rm max}}{ \epsilon_{\rm min}}} }[/math]
if a conjugate gradient, or Quasi-Newton algorithm is chosen. If a good structural start guess exists, the best convergence can be obtained with IBRION=1 and NFREE (number of degrees of freedon) set to a reasonable value. If the initial start guess is bad, it is sometimes required to use the safer conjugate gradient algorithm.
A very important point concerns the required accuracy of the electronic degrees of freedom. If the eigenvalue spectrum of the Hessian matrix is small, EDIFF can be rather large (EDIFF=1E-3). However if the eigenvalue spectrum is broad, EDIFF must be set to a smaller value EDIFF=1E-5, since otherwise the slowly varying degrees of freedom can not be accurately determined in the Hessian matrix. If no convergence is observed for IBRION=1, try to decrease EDIFF.
== I see unphysical oszillations and negative values for the chargedensity in the vacuum. Is VASP not able to give reliable results in the vacuum? ==
VASP gives reliable results, but things are complicated by several issues:
- Avoid, ISMEAR>0, when considering the wavefunctions in the vacuum. It can cause negative occupancies close to the Fermi-level, and since states at the Fermi-level decay slowest in the vacuum, the charge density in the vacuum might be negativ (energies are not effected by this, since the wavefunctions in the vacuum do not contribute significantly to the energy).
- The charge density of self-consistent calculations might have negative values in the vacuum, since the mixer is very insensitive to the charge density in the vacuum. It is better to set LPARD=.TRUE. and call VASP a second time. The generated CHGCAR file contains the chargedensity calculated directly from the wavefunctions.
- In VASP, pseudo charge density components from unbalanced lattice vectors are set to zero: although the charge density is initially calculated in real space and therefore positive definite, it is modified then in reciprocal space, and Fourier transformed back to real space. The final charge density has small oscillations in the vacuum. To avoid this problem, use FFT grids that avoid wrap around errors (PREC=Accurate). The problem can also be reduced by increasing the energy cut off.
- Ultrasoft pseudopotentials require a second support grid. In VASP.4.4.4 and older version, charge density components from unbalanced lattice vectors are also zeroed on the second support grid, causing additional small oscillations in the vacuum. This problem is removed in VASP.4.5 and in VASP.4.4.5. In VASP.4.4.5 the flag -DVASP45 must be specified in the CPP line of the makefile before compiling the VASP code. Total energies might however change by a fraction of a meV.
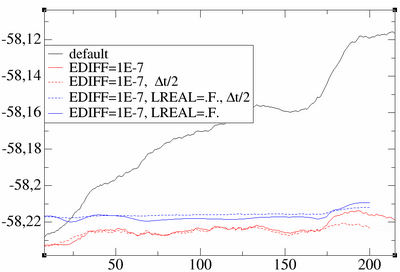
I am running molecular dynamics and observe a large drift in the total energy, that should be conserved.
Three reasons can hamper the energy conservation in VASP.
- First the electronic convergence might not be sufficiently tight. It is often necessary to decrease the tolerance to [math]\displaystyle{ 10^{-6} }[/math] or [math]\displaystyle{ 10^{-7} }[/math] to obtain excellent energy conservation. Alternatively NELMIN can be set to values around 6.
- The second reason is an insufficiently accurate real space projection. This usually causes a slightly spiky and discontinuous total energy. If you observe such a behavior, you have to improve ROPT, or set LREAL=.FALSE.
- Finally, consider reducing the time step.
The following graph illustrates the behavior for a small liquid metallic system (Ti). It shows the energy conservation for a liquid metallic system for various settings. Please mind, that reducing ROPT from -0.002 to -.0005 (LREAL=.A.) had the same effect as using LREAL=.FALSE.
I am running VASP on a SGI Origin, and the simple benchmark.
This issue appears for the benchmark (benchmark.tar.gz) usually with the following message:
lib-4201 : UNRECOVERABLE library error A READ operation tried to read past the end-of-record. Encountered during a direct access unformatted READ from unit 21 Fortran unit 21 is connected to a direct unformatted unblocked file: "TMPCAR" IOT Trap Abort (core dumped)
VASP extrapolates the wave functions between molecular dynamics time steps. To store the wave functions of the previous time steps either a temporary scratch file (TMPCAR) is used (IWAVPR=1-9) or large work arrays are allocated (IWAVPR=11-19). On the SGI, the version that uses a temporary scratch file does not compile correctly, and hence the user has to set IWAVPR to 10.
The parallel performance of VASP is not as good as expected.
What does one mean by performance was not as expected ? Matter of fact, one can never obtain the same scaling on a P3/P4/Athlon XP based workstation cluster as on the T3D. The T3D was a very very slow machine (by todays standard) equipped with an extraordinarily fast network (that's what made the price of the T3D). A Gigabit network has roughly the same overall performance as the T3D (Gigabit has longer latency, larger node-to-node bandwidth, but smaller total aggregated bandwidth), but the P4 CPU is about 10 times faster than one T3D node. Additionally VASP was hot-spot optimized carefully on the T3D.
Altogether VASP will run reasonable efficient on up to 8-16 P4/Athlon XP type nodes (until k-point parallelization is implemented)!
Why is the VASP performance so bad on a dual processor machine?
It is a bad idea to run vasp on dual processor P3/P4/Athlon machines, since two CPU's with small cache have to share the small memory bandwidth (P4 RD-RAMS RIMM based machines are an exception). If you run two serial VASP jobs on such a machine, the performance already drops by 20 %. If you run VASP in parallel, the CPU's have to share additionally one Gigabit card which makes things even worse (the argument, that these two CPUs can exchange data faster, is
irrelevant, since most of the data exchange is not between the two local CPU's).
We are using the LINUX kernel X.X.X and LAM/MPICH X.X.X but VASP fails to run.
First, it must be emphasized that we do NOT SUPPORT VASP on parallel machines (in particular LINUX clusters). This is clearly spelled out in the manual. One reason for this policy is that LINUX systems are too heterogeneous to foresee all possible problems. Most problems are in fact not VASP related but related to very simple basic mistakes made by the system administrator, or complicated inconsistencies between the LINUX kernel and the LAM/MPICH installation, or the compilers and the installed MPICH/LAM version. Such problems can not be solved by us!
But there is no reason to put off quickly.Things have certainly improved a lot in the last few years, and parallel computing is still an area were one kernel/LAM/MPICH upgrade can make a huge difference (both to the better or, unfortunately, to the worse).
Some common failures occurring during the installation of MPICH/LAM should be highlighted:
- The compilation of MPICH/LAM fails: Certainly not a problem we can solve for you. Please contact the MPICH/LAM developers.
- VASP fails to link properly: Make sure that MPICH/LAM was compiled with the same compiler as
used for VASP. Try to adhere strictly to the guidelines in our vasp.4.X makefiles. In particular, it is not possible to link with g77/f77 compiled MPICH/LAM routines, since g77/f77 appends two underscores to MPI_XXXX calls, whereas ifc and pgf90 append only one. Also make sure that the f90 linker uses the proper libraries. This can be achieved usually by using mpif90 or mpif77 as linkers instead of f90. But one needs to make sure that the proper mpif77 front-end is called (try to include the option -v verbose upon calling mpif77). This can be a particular problem on some LINUX installations (SUSE), that install a mpif90 and mpif77 command. Type which mpif90 or which mpif77 to determine which front-end you are using.
- VASP fails to execute properly: LAM requires a daemon to run. It is essential to use a VASP executable and LAM daemon compiled using the same LAM distribution! The problem is related to the one already discussed in the previous section.
- Problems with scaLAPACK: Makefiles for scaLAPACK are not distributed with either scaLAPACK, LAM/MPICH or vasp. One reason for this is that the makefiles depend to some extend on the LAM/MPICH version, on the location of the libraries, on the precisse LINUX distribution etc.
- If you have done everything correctly, and VASP still fails to execute... well, then, you will need to stick to the serial version, or seek professional support from a company distributing or maintaining parallel LINUX clusters.
How to evaluate the total energy properly for and adsorbed ionic species on insulating surface
I adsorb, an ionic species e.g. O[math]\displaystyle{ ^- }[/math] on an insulating surface. To select a specific charge state, I have increased the number of electrons by one compared to the neutral system. Now, I have no clue how to evalute the total energy properly (i.e. are there convergence corrections).
Actually, you MUST NOT set the number of electrons manually for a slab calculation. I.e., when you calculate the slab-O[math]\displaystyle{ ^- }[/math] system you are not allowed to select a specific charge state for the oxygen ion, by increasing the number of electrons manually. Specific charge state calculations make sense only in 3D systems and for cluster calculations.
If you conduct the calculations properly, i.e. if your slab is large enough and the lateral dimension (x,y) of your surface is large enough the energy should converge to the proper value, i.e. the O should acquire the correct charge state automatically.
Reason: If you set the number of electrons in the INCAR file for a slab calculation you end up with a charged slab. The electrostatic energy of such a slab is however only conditionally convergent and worse, in practice, even infinite (basic electrostatics). Therefore, no method whatsoever exists to correct the error in the electrostatic energy. E.g. the energy converges towards infinity, when the vacuum width is increased. You can try to validate this, by simply increasing the vacuum width in VASP for a charged slab. You will find that the energy increases or decreases linearly with the vacuum width.
Well, there is maybe one method that can surmount the aforementioned problem. You can charge the slab and increase systematically the distance between the O[math]\displaystyle{ ^- }[/math] species (by increasing the lateral dimensions of your super cell) at a fixed vacuum width, and finally extrapolate the energies towards infinite lateral distances. The energy should converge towards the correct value as [math]\displaystyle{ 1/d }[/math], where [math]\displaystyle{ d }[/math] is the distance between the adsorbed species. This might yield a converged value. The point is that, as I mentioned above, the electrostatic energy is only conditionally convergent for the case of a charged slab/system, and results depend on how you evaluate the limit towards infinity. However, to the best of my knowledge, this has not been done or attempted hereto (and therefore we can not assist you on that issue).