Dielectric properties of Si using BSE
Overview > Dielectric properties of Si using BSE > Improving the dielectric function > Plotting the BSE fatband structure of Si > List of tutorials
Task
Description: Calculate the dielectric function of Si including excitonic effects by solving the Bethe-Salpeter equation (BSE) on top of GW0.
Input
POSCAR
Si 5.4300 0.5 0.5 0.0 0.0 0.5 0.5 0.5 0.0 0.5 2 cart 0.00 0.00 0.00 0.25 0.25 0.25
INCAR
- This is the INCAR file for the basic DFT calculation:
System = Si PREC = Normal ; ENCUT = 250.0 ISMEAR = 0 ; SIGMA = 0.01 KPAR = 2 EDIFF = 1.E-8
KPOINTS
Automatic 0 Gamma 6 6 6 0 0 0
Calculation
- The workflow of GW0+BSE calculations is given in doall.sh and consists of the following consecutive steps:
- "Standard" DFT groundstate calculation.
- Obtain virtual orbitals: needs WAVECAR file from step 1.
- The GW0 calculation: need WAVECAR and WAVEDER from step 2.
- Optional step: use LOPTICS=.TRUE. to plot dielectric function in the independent particle approximation (IPA) using GW0 quasiparticle energies instead of DFT energies.
- The BSE calculation: needs WAVECAR from step 3 and WAVEDER from step 2.
Step 1: DFT groundstate calculation
- We perform standard DFT calculation using the INCAR.DFT file.
Step 2: Obtain DFT "virtual" orbitals (empty states)
- This step uses the INCAR.DIAG file:
System = Si PREC = Normal ; ENCUT = 250.0 ALGO = EXACT ; NELM = 1 ISMEAR = 0 ; SIGMA = 0.01 KPAR = 2 NBANDS = 128 LOPTICS = .TRUE. ; LPEAD = .TRUE. OMEGAMAX = 40
- We use exact diagonalization for this step (ALGO=EXACT) and keep 128 bands after diagonalization (NBANDS=128).
- With LPEAD=.TRUE. we use an alternative way of computing the derivates of the orbitals with respect to the Bloch wave vectors.
- It is important that this calculations needs the orbitals (WAVECAR file) written in step 1.
Step 3: RPA quasiparticles with single-shot GW (G0W0)
- This step uses the INCAR.GW0 file:
System = Si PREC = Normal ; ENCUT = 250.0 ALGO = GW0 ISMEAR = 0 ; SIGMA = 0.01 ENCUTGW = 150 ; NELM = 1 ; NOMEGA = 50 ; OMEGATL = 280 KPAR = 2 #NBANDSO=4 ; NBANDSV=8 ; LADDER=.TRUE. ; LUSEW=.TRUE. NBANDS = 128 NBANDSGW = 12 LWAVE = .TRUE. PRECFOCK = Normal
- We select the G0W0 method by specifying ALGO=GW0 and NELM=1.
- The energy cut off for the response function is select by ENCUTGW.
- The number of point used in the frequency integration is given by NOMEGA.
- Use the same number of bands (NBANDS) as in step 2, otherwise the WAVEDER file is not read correctly.
- The quasiparticle energies are calculated for the first few bands given by NBANDSGW.
- It is important that this calculation needs the orbitals (WAVECAR file) and the derivatives of the orbitals with respect to the Bloch vectors (WAVEDER file).
- The quasiparticle energies can be found in the OUTCAR file (saved as OUTCAR.GW0 in this example):
QP shifts <psi_nk| G(iteration)W_0 |psi_nk>: iteration 1 for sc-GW calculations column KS-energies equals QP-energies in previous step and V_xc(KS)= KS-energies - (<T + V_ion + V_H > + <T+V_H+V_ion>^1 + <V_x>^1) k-point 1 : 0.0000 0.0000 0.0000 band No. KS-energies QP-energies sigma(KS) V_xc(KS) V^pw_x(r,r') Z occupation
Step 4 (optional): Plot IPA dielectric function using GW0 quasiparticle energies
- This step uses the INCAR.NONE file:
System = Si PREC = Normal ; ENCUT = 250.0 ALGO = Nothing ; NELM = 1 ISMEAR = 0 ; SIGMA = 0.01 KPAR = 2 NBANDS = 128 LWAVE = .FALSE. LOPTICS = .TRUE. ; LPEAD = .TRUE. OMEGAMAX = 40
- By specyfing ALGO=Nothing we do nothing except reading the WAVECAR file.
- Using LOPTICS=.TRUE. and LPEAD=.TRUE. we compute the dielectric function in the IPA.
Step 5: The BSE calculation
- This step uses the INCAR.BSE file:
PREC = Normal ; ENCUT = 250.0 ALGO = BSE ANTIRES = 0 ISMEAR = 0 ; SIGMA = 0.01 ENCUTGW = 150 EDIFF = 1.E-8 NBANDS = 128 NBANDSO = 4 NBANDSV = 8 OMEGAMAX = 20 PRECFOCK = Normal
- By specifying ANTIRES=0 we use the Tamm-Dancoff approximation.
- ENCUTGW=150 specifies the energy cut-off of the response function.
- NBANDSO and NBANDSV define the number of valence and conduction bands in the calculations.
- This calculation needs the orbitals (WAVECAR file) from step 3 and the derivative of the orbitals with respect to the Bloch vectors (WAVEDER file) written in step 2.
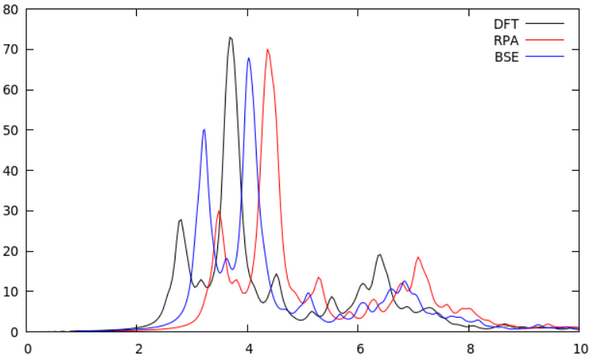
- By using the script ./plotall.sh we get the absorption spectra within the independent particle picture and with BSE:
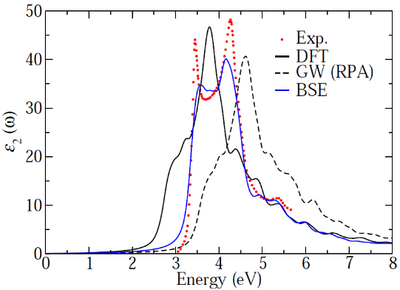
- The calculated dielectric function of Si is at this point (GW+BSE) already in much better agreement with experiment. However we can do even better as shown in the following figure:
- The problem comes from the coarse k-point grid that we have used. A denser grid samples more (direct) transitions between the bands.
- Simply using a denser grid is mostly not an option because of the computational expense.