Plotting the BSE fatband structure of Si: Difference between revisions
| Line 127: | Line 127: | ||
*The sample output for this tutorial should look like the following: | *The sample output for this tutorial should look like the following: | ||
[[File:Fig BSE example3 1.png|500px]] | [[File:Fig BSE example3 1.png|500px]] | ||
The fat band picture allows you to visually inspect which e-h pairs contribute the most to a particular BSE eigenstate. When k-point convergence is important, you can use it to truncate your e-h product basisset by choosing smarter {{TAG|NBANDSO}}/{{TAG|NBANDSV}} and/or {{TAG|OMEGAMAX}} values. | |||
Try {{TAG|NBANDSO}}={{TAG|NBANDSV}}=2and check how much this effects the BSE results. | |||
== Download == | == Download == | ||
Revision as of 16:10, 14 December 2017
Task
Visualization of BSE eigenvectors using fatbands.
Input
Si 5.4300 0.5 0.5 0.0 0.0 0.5 0.5 0.5 0.0 0.5 2 cart 0.00 0.00 0.00 0.25 0.25 0.25
INCAR
- This is the INCAR file for the basic DFT calculation:
System = Si PREC = Normal ; ENCUT = 250.0 ISMEAR = 0 ; SIGMA = 0.01 KPAR = 2 EDIFF = 1.E-8 NBANDS = 16 LOPTICS = .TRUE. # needed for WAVEDER file LPEAD = .TRUE. OMEGAMAX = 40
KPOINTS
The KPOINTS file will be automatically generated in this example.
Calculation
- In this example we will calculate and plot the first "bright" BSE eigenstates of silicon, also called fatbands[1]. In this tutorial the modelBSE setup from the previous tutorial is used in combination with a gamma centered k-point grid (if you don't want to wait that long, a grid takes only a minute). In principle the standard BSE method can also be used instead.
Step 1 DFT calculation
We run a standard DFT calculation with the input files given above.
Step 2 BSE calculation with fatbands
- The INCAR file for the modelBSE calculation looks like the following:
System = Si PREC = Normal ; ENCUT = 250.0 #ALGO = BSE ANTIRES = 0 ISMEAR = 0 ; SIGMA = 0.01 ENCUTGW = 150 EDIFF = 1.E-8 # default 1.E-4 NBANDS = 16 # only bands that are used are required, prepare the same set in a forgoing DFT run NBANDSO = 4 NBANDSV = 8 OMEGAMAX = 20 PRECFOCK = Normal ALGO = TDHF LMODELHF = .TRUE. #Turn model on HFSCREEN = 1.26 # Screening lenght AEXX = 0.088 #Inverse of epsilon_infinity SCISSOR = 0.69 # Difference GW-DFT band gap NBSEEIG = 10 # number of BSE eigenvectors written out in BSEFATBAND
- The important tag for fatband calculations is NBSEEIG. In this example this will write the 10 energetically lowest BSE eigenvectors to the output file BSEFATBAND.
- After the (model)BSE calculation we first look into the vasprun.xml file to have a look at the BSE eigenvalues and the oscillator strengths (exact numbers can of course differ depending on the method you use and the density of your k-point grid):
<varray name="opticaltransitions" >
<v> 3.148 0.000 </v>
<v> 3.148 0.000 </v>
<v> 3.148 0.000 </v>
<v> 3.149 25654.244 </v>
<v> 3.149 25660.601 </v>
<v> 3.149 25665.652 </v>
<v> 3.151 0.001 </v>
<v> 3.151 0.001 </v>
<v> 3.152 423.751 </v>
<v> 3.310 216931.963 </v>
<v> 3.310 216916.814 </v>
<v> 3.310 216935.593 </v>
The first number column shows the BSE eigenvalue and the second one the oscillator strength. We want to plot the first "bright" state, that means in this case number 4.
- We inspect the fourth band in the BSEFATBAND output file:
28428 10
1BSE eigenvalue 3.14798542 IP-eigenvalue: 3.25790292
0.00000 0.00000 0.00000 -6.1302666 9.0994773 0.0000001 1 5 -0.000000+i* -0.000000
0.00000 0.00000 0.00000 5.8415744 9.0994773 0.0876503 2 5 0.000076+i* 0.000043
0.00000 0.00000 0.00000 5.8415744 9.0994773 341.0850802 3 5 0.088630+i* -0.329369
0.00000 0.00000 0.00000 5.8415744 9.0994773 543.1678695 4 5 0.361803+i* -0.405130
0.00000 0.00000 0.00000 -6.1302666 9.0994773 0.0000004 1 6 -0.000000+i* 0.000000
…(28428-6 more lines till 2BSE eigenvalue …)
4BSE eigenvalue 3.14855812 IP-eigenvalue: 3.25790292
0.00000 0.00000 0.00000 -6.1302666 9.0994773 0.0024165 1 5 0.000002+i* 0.000001
0.00000 0.00000 0.00000 5.8415744 9.0994773 31.4738813 2 5 -0.027821+i* -0.014718
0.00000 0.00000 0.0000File:Fig BSE example3 1.png0 5.8415744 9.0994773 187.8684774 3 5 0.049093+i* -0.181341
0.00000 0.00000 0.00000 5.8415744 9.0994773 360.1697144 4 5 0.239775+i* -0.268757
0.00000 0.00000 0.00000 -6.1302666 9.0994773 0.0289534 1 6 0.000019+i* -0.000022
...
The description of the values is given as follows:
- line: Number of e-h pairs in the BSE basis and value for NBSEEIG.
- line: BSE eigenvalue and minimum band gap before BSE.
- line: Column 1-3 k-point coordinate, column 4 hole eigenvalue, column 5 electron eigenvalue, column 6 absolute value of coupling coefficient (radius of circles), column 7 hole orbital, column 8 electron number, column 9 real part of coupling coefficient, column 10 imaginary part of coupling coefficient.
Columns 1-6 are used to plot the fatbands.
- Plotting of data:
- Select the BSE eigenstate from the FATBAND file which you want to plot.
- Filter out all e-h pairs that lie on the high symmetry k-lines along which you want to plot the fat bandstructure:
#!/bin/bash
head -n 113716 BSEFATBAND > tmp.dat
tail -n 28428 BSEFATBAND > BSE4.dat
rm tmp.dat
awk <BSE4.dat ' { if ($1==$2 && $3==$2) print sqrt($1*$1+$2*$2+$3*$3), $4, $5, $6 }' >bands-GL.dat
awk <BSE4.dat ' { if ($1==$3 && $2==0.0) print sqrt($1*$1+$2*$2+$3*$3), $4, $5, $6 }' >bands-GX.dat
- Use your favourite tool to plot the output in the following manner:
|k-point| electron hole |A|
eigenvalue eigenvalue
x y1 y2 radius
File:Fig BSE example3 1.png
- The sample output for this tutorial should look like the following:
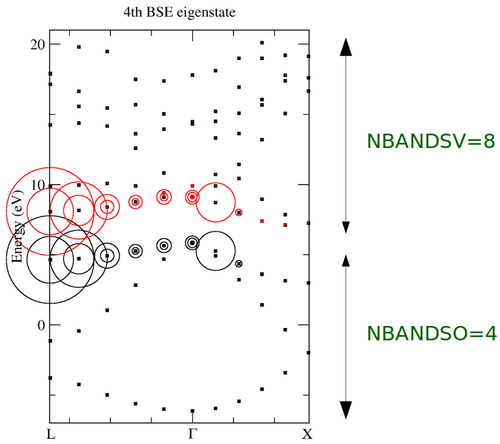 The fat band picture allows you to visually inspect which e-h pairs contribute the most to a particular BSE eigenstate. When k-point convergence is important, you can use it to truncate your e-h product basisset by choosing smarter NBANDSO/NBANDSV and/or OMEGAMAX values.
Try NBANDSO=NBANDSV=2and check how much this effects the BSE results.
The fat band picture allows you to visually inspect which e-h pairs contribute the most to a particular BSE eigenstate. When k-point convergence is important, you can use it to truncate your e-h product basisset by choosing smarter NBANDSO/NBANDSV and/or OMEGAMAX values.
Try NBANDSO=NBANDSV=2and check how much this effects the BSE results.
Download
References
Back to the main page


