Calculate U for LSDA+U
Task
In this exercise, you will calculate the U parameter for the DFT+U treatment of Ni d-electrons in NiO using the linear response ansatz of Cococcioni et al..[1]
POSCAR
For this calculation we will use a 2×2×2 supercell of AFM-II NiO:
AFM NiO 4.03500000 2.0000000000 1.0000000000 1.0000000000 1.0000000000 2.0000000000 1.0000000000 1.0000000000 1.0000000000 2.0000000000 1 15 16 Direct 0.0000000000 0.0000000000 0.0000000000 0.2500000000 0.2500000000 0.2500000000 0.0000000000 0.0000000000 0.5000000000 0.2500000000 0.2500000000 0.7500000000 0.0000000000 0.5000000000 0.0000000000 0.2500000000 0.7500000000 0.2500000000 0.0000000000 0.5000000000 0.5000000000 0.2500000000 0.7500000000 0.7500000000 0.5000000000 0.0000000000 0.0000000000 0.7500000000 0.2500000000 0.2500000000 0.5000000000 0.0000000000 0.5000000000 0.7500000000 0.2500000000 0.7500000000 0.5000000000 0.5000000000 0.0000000000 0.7500000000 0.7500000000 0.2500000000 0.5000000000 0.5000000000 0.5000000000 0.7500000000 0.7500000000 0.7500000000 0.1250000000 0.1250000000 0.1250000000 0.3750000000 0.3750000000 0.3750000000 0.1250000000 0.1250000000 0.6250000000 0.3750000000 0.3750000000 0.8750000000 0.1250000000 0.6250000000 0.1250000000 0.3750000000 0.8750000000 0.3750000000 0.1250000000 0.6250000000 0.6250000000 0.3750000000 0.8750000000 0.8750000000 0.6250000000 0.1250000000 0.1250000000 0.8750000000 0.3750000000 0.3750000000 0.6250000000 0.1250000000 0.6250000000 0.8750000000 0.3750000000 0.8750000000 0.6250000000 0.6250000000 0.1250000000 0.8750000000 0.8750000000 0.3750000000 0.6250000000 0.6250000000 0.6250000000 0.8750000000 0.8750000000 0.8750000000
Atoms 1-16 are Ni, and atoms 17-32 are O.
Note that the Ni atoms are split into two groups: atom 1, and atom 2-15. This trick breaks the symmetry of the Ni sub-lattice and allows us to treat atom 1 differently from atom 2-15. Our POTCAR file has to reflect the fact that we now formally have 3 "species" (2 ×Ni + 1×O), i.e., we concatenate two Ni POTCAR files and one O POTCAR file:
cat Ni/POTCAR Ni/POTCAR O/POTCAR > POTCAR
To check whether you have a suitable POTCAR type:
grep TITEL POTCAR
This should yield something like:
TITEL = PAW Ni 02Aug2007 TITEL = PAW Ni 02Aug2007 TITEL = PAW O 22Mar2012
i.e., two Ni entries followed by one O entry.
KPOINTS
Gamma only 0 Monkhorst 1 1 1 0 0 0
The DFT groudstate
We will calculate the DFT ground state of our NiO system with the following INCAR:
SYSTEM = NiO AFM PREC = A EDIFF = 1E-6 ISMEAR = 0 SIGMA = 0.2 ISPIN = 2 MAGMOM = 1.0 -1.0 1.0 -1.0 \ 1.0 -1.0 1.0 -1.0 \ 1.0 -1.0 1.0 -1.0 \ 1.0 -1.0 1.0 -1.0 \ 16*0.0 LORBIT = 11 LMAXMIX = 4
Instrumental here is that we correctly specify the initial magnetic moments (by means of MAGMOM-tag). The setting above is consistent with the AFM-II magnetic structure: alternating ferromagnetic Ni (111)-layers.
Secondly, we set LORBIT=11: at the end of the OUTCAR file, VASP will write the number of (d-) electrons per site. This information we will need to compute the U-parameter.
Last but not least, we set LMAXMIX=4: this is needed to be able to perform non-selfconsistent (ICHARG=11) DFT+U calculations (LDAUTYPE=3) in the following. For this reason we will keep a copy of the CHGCAR file (and the WAVECAR file as well):
cp CHGCAR CHGCAR.0 cp WAVECAR WAVECAR.0
The information most relevant to the task at hand you will find near the end of the OUTCAR file:
total charge
# of ion s p d tot
------------------------------------------
1 0.342 0.490 8.439 9.270
2 0.342 0.490 8.438 9.269
3 0.342 0.490 8.438 9.270
4 0.342 0.490 8.438 9.269
5 0.342 0.490 8.438 9.270
6 0.342 0.490 8.438 9.269
7 0.342 0.490 8.438 9.269
8 0.342 0.490 8.438 9.269
9 0.342 0.490 8.438 9.270
10 0.342 0.490 8.438 9.269
11 0.342 0.490 8.438 9.269
12 0.342 0.490 8.438 9.269
13 0.342 0.490 8.438 9.269
14 0.342 0.490 8.438 9.269
15 0.342 0.490 8.438 9.269
16 0.342 0.490 8.438 9.269
17 1.564 3.455 0.000 5.019
18 1.564 3.455 0.000 5.019
.
.
.
magnetization (x)
# of ion s p d tot
------------------------------------------
1 0.001 -0.020 1.098 1.079
2 -0.001 0.020 -1.098 -1.080
3 0.001 -0.020 1.098 1.079
4 -0.001 0.020 -1.098 -1.080
5 0.001 -0.020 1.098 1.079
6 -0.001 0.020 -1.098 -1.080
7 0.001 -0.020 1.098 1.080
8 -0.001 0.020 -1.098 -1.080
9 0.001 -0.020 1.098 1.079
10 -0.001 0.020 -1.098 -1.080
11 0.001 -0.020 1.098 1.080
12 -0.001 0.020 -1.098 -1.080
13 0.001 -0.020 1.098 1.080
14 -0.001 0.020 -1.098 -1.080
15 0.001 -0.020 1.098 1.080
16 -0.001 0.020 -1.098 -1.080
17 -0.000 0.000 0.000 0.000
18 0.000 -0.000 0.000 -0.000
19 0.000 -0.000 0.000 -0.000
.
.
.
This shows that in the DFT grounstate mostlyd-electrons are attributed to atomic sites 1-16 with anti-ferromagnetic ordering.
Non-selfconsistent response
The next step is to calculate the following response function:
- [math]\displaystyle{ \chi^0_{IJ}=\frac{\partial N^{\rm NSCF}_{I}}{\partial V_{J}} }[/math]
This is the change in the number of d-electrons on site I due to an additional spherical potential acting on the d-manifold on site J. In the following we will assume this response to be zero unless I=J.
To add an additional spherical potential on the site of atom 1 that acts on the d-manifold we specify the following:
LDAU = .TRUE. LDAUTYPE = 3 LDAUL = 2 -1 -1 LDAUU = 0.10 0.00 0.00 LDAUJ = 0.10 0.00 0.00
Note that for LDAUTYPE=3 the LDAUU and LDAUJ tags specify the strength (in eV) of the spherical potential acting on the spin-up and spin-down d-manifolds, respectively.
In the present step, we want to calculate the non-selfconsistent response to this additional potential. This is done by reading the charge density from the previous DFT ground-state calculations and by keeping it fixed during the electronic minimization procedure:
ICHARG = 11
N.B.: be sure to use the charge density of the DFT groundstate calculation:
cp CHGCAR.0 CHGCAR cp WAVECAR.0 WAVECAR
After running this calculation, you will notice that due to the additional potential, the number of d-electrons on atom 1 has changed w.r.t. the DFT groundstate (check the OUTCAR file again):
total charge
# of ion s p d tot
------------------------------------------
1 0.342 0.490 8.488 9.319
2 0.342 0.489 8.432 9.263
3 0.342 0.490 8.438 9.269
4 0.342 0.490 8.438 9.269
5 0.342 0.490 8.438 9.269
6 0.342 0.490 8.438 9.269
7 0.342 0.490 8.435 9.266
8 0.342 0.490 8.438 9.269
9 0.342 0.490 8.438 9.269
10 0.342 0.490 8.438 9.269
11 0.342 0.490 8.435 9.266
12 0.342 0.490 8.438 9.269
13 0.342 0.490 8.435 9.266
14 0.342 0.490 8.438 9.269
15 0.342 0.490 8.430 9.261
16 0.342 0.489 8.432 9.263
17 1.564 3.455 0.000 5.019
18 1.564 3.455 0.000 5.018
19 1.564 3.454 0.000 5.018
20 1.564 3.454 0.000 5.018
21 1.564 3.454 0.000 5.018
22 1.564 3.454 0.000 5.018
23 1.564 3.454 0.000 5.018
24 1.564 3.454 0.000 5.018
25 1.564 3.454 0.000 5.018
26 1.564 3.454 0.000 5.018
27 1.564 3.454 0.000 5.018
28 1.564 3.454 0.000 5.018
29 1.564 3.454 0.000 5.018
30 1.564 3.454 0.000 5.018
31 1.564 3.455 0.000 5.018
32 1.564 3.455 0.000 5.019
--------------------------------------------------
tot 30.488 63.101 135.027 228.617
The change in the number of d-electrons on atomic site 1 is found to be:
- [math]\displaystyle{ \Delta N^{\rm NSCF}_1= 4.488 - 4.438 = 0.050 }[/math]
and hence
- [math]\displaystyle{ \chi^0_{11} = \frac{0.050}{0.1} = 0.50 \; (eV)^{-1} }[/math]
Selfconsistent response
The selfconsistent reponse function:
- [math]\displaystyle{ \chi_{IJ}=\frac{\partial N^{\rm SCF}_{I}}{\partial V_{J}} }[/math]
is computed similarly:
LDAU = .TRUE. LDAUTYPE = 3 LDAUL = 2 -1 -1 LDAUU = 0.10 0.00 0.00 LDAUJ = 0.10 0.00 0.00
N.B.I: The only difference between this calculation and the previous calculation of the non-selfconsistent response is that now we do not set ICHARG=11, i.e, now the charge density may change.
N.B.II: To speed things up, it is a good idea to restart this calculation from the WAVECAR file of the previous non-selfconsistent response calculation.
After this calculation has finished, you should again inspect the number of d-electrons on atomic site 1:
total charge
# of ion s p d tot
------------------------------------------
1 0.341 0.488 8.452 9.281
2 0.342 0.490 8.438 9.269
3 0.342 0.490 8.438 9.269
4 0.342 0.490 8.438 9.269
5 0.342 0.490 8.438 9.269
6 0.342 0.490 8.438 9.269
7 0.342 0.490 8.438 9.269
8 0.342 0.490 8.438 9.269
9 0.342 0.490 8.438 9.269
10 0.342 0.490 8.438 9.269
11 0.342 0.490 8.438 9.269
12 0.342 0.490 8.438 9.269
13 0.342 0.490 8.438 9.269
14 0.342 0.490 8.438 9.269
15 0.342 0.490 8.438 9.269
16 0.342 0.490 8.438 9.269
17 1.564 3.455 0.000 5.019
18 1.564 3.455 0.000 5.019
19 1.564 3.455 0.000 5.018
20 1.564 3.455 0.000 5.019
21 1.564 3.455 0.000 5.018
22 1.564 3.455 0.000 5.019
23 1.564 3.455 0.000 5.019
24 1.564 3.455 0.000 5.018
25 1.564 3.455 0.000 5.018
26 1.564 3.455 0.000 5.019
27 1.564 3.455 0.000 5.019
28 1.564 3.455 0.000 5.018
29 1.564 3.455 0.000 5.019
30 1.564 3.455 0.000 5.018
31 1.564 3.455 0.000 5.019
32 1.564 3.455 0.000 5.019
--------------------------------------------------
tot 30.488 63.107 135.022 228.617
The change in the number of d-electrons on atomic site 1 is found to be:
- [math]\displaystyle{ \Delta N^{\rm NSCF}_1= 4.452 - 4.438 = 0.012 }[/math]
and hence
- [math]\displaystyle{ \chi_{11} = \frac{0.012}{0.1} = 0.12 \; (eV)^{-1} }[/math]
The final result
After we have computed both the non-selfconsistent as well as the selfconsistent response functions, the U parameter for the DFT+U treatment of Ni d-electrons in NiO is found from:
[math]\displaystyle{ U = \chi^{-1}-\chi_0^{-1} \approx \left(\frac{\partial N^{\rm SCF}_{I}}{\partial V_{I}}\right)^{-1} - \left(\frac{\partial N^{\rm NSCF}_{I}}{\partial V_{I}}\right)^{-1} = \frac{1}{0.12}-\frac{1}{0.5} = 6.33 \; eV }[/math]
To get a more accurate result, one should repeat the previous calculations for a series of different additional potentials (for instance, LDAUU = LDAUJ = -0.2, -0.15, -0.10, -0.05, 0.05, 0.10 ,0.15, and 0.20 eV). All necessary steps are scripted in doall.sh in the tgz-file below.
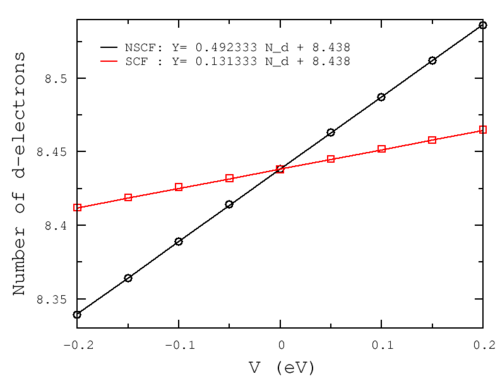
The relevant response functions are then easily found from a linear fit of the number of d-electrons on atomic site 1 as a function of the additional potential V:
From the above, we then have:
[math]\displaystyle{ U = \chi^{-1}-\chi_0^{-1} \approx \left(\frac{\partial N^{\rm SCF}_{I}}{\partial V_{I}}\right)^{-1} - \left(\frac{\partial N^{\rm NSCF}_{I}}{\partial V_{I}}\right)^{-1} = \frac{1}{0.131333}-\frac{1}{0.492333} = 5.58 \; eV }[/math]